Математическое моделирование. Динамические и статистические системы, страница 12

          Пусть при  оба значения  являются чисто мнимыми и при этом 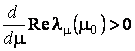. В этом случае  является точкой бифуркации: в интервале ;  при всех  начало координат является устойчивым фокусом, при всех ,  начало координат – неустойчивый фокус, окруженный предельным циклом, размер которого растет с увеличением . Второй случай означает, что траектория системы выходя из начальной точки с течением времени переходит на стационарную траекторию в фазовом пространстве (например, переходит в режим колебаний).

          Возможно и такое развитие системы, когда с изменением управляющего параметра число бифуркаций непрерывно возрастает в конечном счете система переходит к сложному стохастическому поведению, при котором фазовые траектории системы втягиваются в область состояний, называемую странным аттрактором. Две близкорасположенные вначале фазовые траектории с течением времени расходятся существенно непредсказуемым образом, так что наш первоначальное знание превращается в полное незнание. Система переходит от простого динамического поведения к сложному стохастическому.

          Фейгенбаум показал, что несмотря на индивидуальность систем сценарии их эволюции от простого детерминированного поведения одинаковы: через «древо» бифуркации к странному аттрактору. Типичной системой со странным аттрактором является система Лоренца, моделирующая конвективные процессы:

где s, b, r – безразмерные величины (критерии подобия), переменные X, Y, Z определяют вертикальную компоненту поля скоростей и поле температурных отклонений. Аналогично выглядят уравнения одномодового лазера для напряженности поля E, поляризации P и инверсии D.

          Математический анализ показал, что наиболее логичное исследование типов странных аттракторов можно провести, если ввести в рассмотрение пространства дробной размерности. Фактически это означает переход к формам симметрии более высокого порядка.

          Множество с дробной размерностью принято называть фракталами. Теория фрактальных множеств пока еще ждет развития в практических приложениях.

4.9 Математический эксперимент

          Математический эксперимент в настоящее время занимает прочные позиции в инженерных исследованиях. Проблемам этой сферы деятельности посвящена достаточно обширная литература и в качестве доступного источника можно предложить [42].

          Выше (см. стр.75) было сказано о математическом эксперименте Ферми, Пасты, Улама.

          Впечатляющий математический эксперимент был поставлен Н. Н. Моисеевым. Суть его в следующем. Существует известное решение Пуазейля о движении жидкости в трубах. Была поставлена задача, существуют ли другие  решения уравнения Навье - Стокса и как они могут быть связаны с течением Пуазейля. Известно, что течение Пуазейля существует для любых расходов Q, меньших некоторого критического значения Q_кр. При Q ³ Q_кр оно теряет устойчивость. Машинный эксперимент показал, что при любых начальных условиях при Q < Q_кр при t ® ¥  течение стремится к течению Пуазейля. С увеличением величины Q эта тенденция становилась все менее ярко выраженной. Была предпринята попытка найти другие стационарные решения, но они не обнаружились, но обнаружился целый класс почти периодических решений. В процессе математического эксперимента выяснилось, что для обеспечения такого режима течения необходим перепад давления значительно больший, чем при течении Пуазейля. Известно, что если допускается существование двух процессов с одним и тем же результатом, то реализуется тот процесс, который требует наименьших энергетических затрат (принцип минимума диссипации энергии).