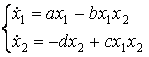Математическое моделирование. Динамические и статистические системы, страница 3

.

          Как видим, система является нелинейной.

          Проведем исследование полученной модели. Легко видеть, что система имеет две особых точки (0,0) и . Используя методы теории устойчивости можно установить, что первая точка является седлом, а вторая точка типа – центр. Поэтому система являясь устойчивой, не является асимптотически устойчивости.

          Разделим почленно первое уравнение на второе и получим первый интеграл системы.

;

или                                            ,

где                             ;        .

          Уравнение Вольтерра - Лоттки является стандартной моделью и по ее типу возможно построение моделей для описания конкурирующих подсистем.

          Рассмотренное нами уравнение Вольтерра - Лоттки предполагает, что изменение состояния  связано с состояниями  и  в один и тот же момент времени, аналогичное замечание можно сделать и для второй компоненты системы. Такое приближение называется адиабатным.

          Чтобы смысл сделанного замечания был понятен, рассмотрим уравнение динамики камеры сгорания ЖРД.         Простейшее уравнение (модель) процесса можно составить из условия сохранения вещества:

;

где Q – масса газа в камере сгорания (КС);  – скорость образования продуктов сгорания в топливе;  – масса продуктов сгорания, вылетающих через сопло. В простейшем случае (нулевое приближение) можно предположить, что , где  – масса горючего и окислителя, поступающих в момент t в КС через форсуночную головку КС.

          Такая постановка вопроса предполагает, что сгорание топлива протекает мгновенно, а на подготовку и течение процесса окисления время не затрачивается. Учитывая, что , где A – комплексный коэффициент подачи топлива и окислителя;  – давление в системе подачи топлива и окислителя;  – давление, соответствующее стационарному процессу.

          Как следует из уравнения состояния идеального газа 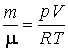 и уравнения динамики КС в нулевом приближении может быть записано в виде:

.

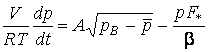          В этом уравнении  – площадь критического сечения сопла и b – расходный комплекс (все прочие обозначения – стандартные). Однако, если учитывать, что на подготовку топливной смеси и протекания реакции затрачивается некоторое время, то необходимо ввести в рассмотрение кривую выгорания и соответствующее ей время запаздывания t. В результате мы придем к уравнению:

.

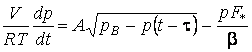          Это уравнение относится к классу уравнений с запаздывающим аргументом: скорость изменения состояния зависит не только от состояния системы в данный момент времени, но также и от состояния в предыдущий момент времени.

          Хорошо известно логистическое уравнение, моделирующее динамику непересекающихся поколений насекомых: