Математическое моделирование. Динамические и статистические системы, страница 13

          Принцип минимума диссипации энергии выделяет реализуемое природой движение из всех виртуальных движений. Природа из всех движений выделяет не просто те движения, при которых энтропия растет, а только те, при которых рост энтропии минимален. В конечном счете удалось подойти к построению приближенного представления турбулентного течения и удалось показать, что оно генетически связано с законами сохранения.

          Таким образом, математический эксперимент позволяет не только численно решить поставленную задачу, но и сделать глубокие обобщающие выводы.

          Современный математический эксперимент, тесно связанный с инженерной практикой, обычно строится для решения задач, когда начальная информация о явлении уже имеется.

          Методика его постановки достаточно ясна. Строится математический образ объекта или явления в поле внешних факторов, при этом в процессе численного анализа с помощью ЭВМ создается определенная картина поведения объекта при изменяющихся внешних условиях. Выделим несколько удачных, наглядных примеров, представленных в литературе последнего времени.

          В работе [50] проводится исследование влияния неравномерности вращения ротора газотурбинного двигателя на колебания рабочих лопаток. Такого рода ситуации возникают при разгоне ротора газотурбинного двигателя (ГТД) во время запуска или при переходе двигателя с одного режима на другой.

          В качестве объекта исследования взят класс лопаток ГТД, которые в границах данной задачи можно рассматривать как прямоугольные пластины, установленные параллельно оси вращения ротора.

          Математический образ модели строится на основе фундаментального уравнения теории упругости:

,

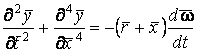при граничных условиях

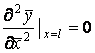
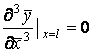
где ; ; ; ; ; ;

  – масса лопатки; w – угловая скорость ротора; l – длина лопатки; E – модуль Юнга; r – плотность материала лопатки; I – момент инерции поперечного сечения; S – площадь поперечного сечения; y – прогиб лопатки; x – координата поперечного сечения.

          Т.к. базовое уравнение в исходном виде не может быть проинтегрировано, то построим математический образ лопатки, представив ее как закрепленный на диске радиуса  r⁽ⁿ⁾  невесомый стержень с сосредоточенными массами , которые удалены от диска лопатки на расстояния  соответственно.

          Модели, представленные на рис.17-18 соответствует уравнение

;

;

; ; ; ; ;

 – отклонение массы  от положения, при котором стержень не деформирован;  – отклонение массы  пол действием единичной силы, приложенной к массе  при . Мы сохранили в основном обозначения авторов. Интегрирование системы дифференцируемых уравнений, описывающих модель, приводит авторов к выводам, имеющим принципиальное практическое значение.