Математическое моделирование. Динамические и статистические системы, страница 2

4.3 Принципы построения физико-математических моделей

          Безусловно, невозможно указать какой-либо алгоритм формирования математических моделей систем. Математическая модель – это как бы математический образ реальности и вполне естественно, что этот образ беднее самой реальности. Но модель должна достаточно адекватным образом отражать все необходимые внутренние и внешние связи функционирования системы.

          Первый шаг в формировании модели – выделение всех структурных составляющих системы по принципу, что движение всей системы определяется движением каждого ее элемента и движение каждого элемента системы зависит от поведения всех остальных.

          Второй шаг заключается в выявлении всех существенных и необходимых связей между элементами системы прямых и обратных. В механических системах соответствующие прямой и обратной связей регламентируется очень просто: это третий закон Ньютона – действие равно противодействию. Это обратная связь линейна по своей природе и такой характер обратных связей вписывается в идеологию всего классического естествознания, согласно которой нелинейность – это «испорченная» линейность.

          Третий шаг – самый ответственный. Заменяем реальные связи их математическими образами. В этом плане следует ориентироваться на сложившиеся традиции моделирования, т.к. они отражают уже накопленный опыт исследований, проверенный практикой. Рассмотрим некоторые показательные примеры из этой сферы.

4.4 Уравнения Вольтерра – Лоттки

          Уравнения Вольтерра - Лоттки моделируют взаимоотношения в системе рыб: хищники – жертвы. Первоначально эта модель использовалась для объяснения осцилляций количества рыбы в Адриатическом море. Вполне очевидно, что авторы модели исходили из тезиса, что основу существования популяций составляет удовлетворение 2-х основных потребностей: в пище и размножении при выводе уравнений мы положим в качестве исходных именно это положение.

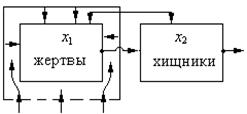
Рис. 13. Динамика взаимосвязей

          Сформируем цепочки питания и обратных связей в популяциях.

          Популяция рыбы – жертвы: численность популяции x первичная цепочка питания – открытая система ресурс, которой неограничен, т.е. считаем пропускную способность среды бесконечно большой. Принятие этой модели окружающей среды допускает рост популяции x₁, по закону геометрической прогрессии ax₁, в тоже время убыль популяции определяется не столько численностью ее самой, сколько численностью x₂ популяции хищников, для которых популяция x₁ является первичной цепочкой питания. Поэтому убыль популяции x₁ будет пропорциональна .

          Составляем динамическую модель по типу ;

уравнение скорости изменения  определится балансом между размножением и потерями, в связи с чем первое уравнение системы запишется

.

          Для популяции рыб – хищников x₂ прирост определяется наличием x₁ как первичной для x₂ цепочки питания, поэтому прирост населения хищников зависит как от численности x₂, так и от численности x₁, т.е. прирост составит cx₁x₂, а естественная убыль при условии, что популяция x₂ автономна, и на ее численности не сказывается эффекты промысла или уничтожения хищников другими хищниками будет пропорциональна численности x₂ (и составит – dx₂).

          Итак, запишем уравнение Вольтерра - Лоттки: