Математическое моделирование. Динамические и статистические системы, страница 6

;  ;  ;  ;  ;  .

          Профиль определяемого ребра представлен на рисунке 15.

Очевидным недостатком найденного профиля является его острая кромка. Тем не менее полученное решение может служить основой для инженерного прообраза, если толщину ребра ограничить некоторой минимальной величиной. Соответствующие указания к расчетам приведены в литературе.

        Полезно также рассмотреть задачу и ребре теплообменника, функционирующего в условиях естественной конвекции. Эта задача приводится ниже.

Задача о ребре теплообменника, функционирующего в условиях

естественной конвекции

          В соответствии с законами теплообмена уравнение энергии в этом случае имеет вид:

,

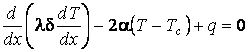где  – коэффициент теплоотдачи; Т_с – температура среды.

          Задача об определении оптимального профиля теплоотводящего ребра сводится к расчету функционала

.

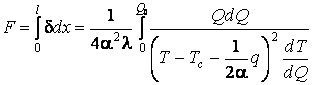          Уравнение Эйлера соответствующей вариационной задачи имеет вид

,

а его решением будет функция

.

          Константы С₁ и С₂ определяются из граничных условий:

;   ;   .

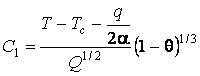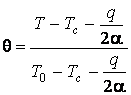          Расчет функционала дает:

.

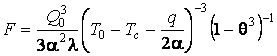          Для теплоотводящего ребра , следовательно для оптимального ребра .

          Отсюда следует:                 ;     .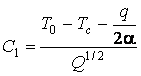

          Для температуры ребра получается выражение

.

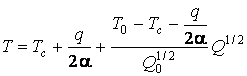          Для оптимального профиля ребра получаем

.

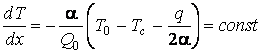          Таким образом наивыгоднейшему по весу ребру отвечает ребро с постоянным температурным градиентом.

4.5 Математика в социально-экономических ситуациях

          Сфера материального производства и тесно связанная с ней сфера экономики представляют собой области, где «покой нам только снится». Эти две наиболее динамичные подсистемы общественного процесса не могут замереть в каком-то стабильном устойчивом состоянии, они по природе своей должны находится в движении.

          На разных срезах экономики использование математических моделей является не столько полезным, сколько необходимым, потому что без математики невозможно указать реальное положения дел и тем более невозможно сделать какие-либо прогнозы.

          Какова особенность анализируемой сферы приложения математики?

          Если инженер конструирует какую-либо систему, то в свой проект он закладывает пространство возможных фазовых состояний системы.