Информатика и выч. техника \ Основы информатики и вычислительной техники

Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 7

Случайный сигнал описывается статистически с помощью различных вероятностных характеристик.

Предположим, что имеется  N реализаций случайного сигнала. Зафиксировав аргумент t (t = ti) получим N значений случайной величины ξ.

Задание вероятностей ее возможных значений эквивалентно заданию так называемой функции распределения (интегрального закона) Fξ(x,ti). Значение функции распределения Fξ(x,ti) в точке х есть вероятность того, что случайная величина ξ примет значение меньшее или равное х, т.е.

                                (1.1)

 


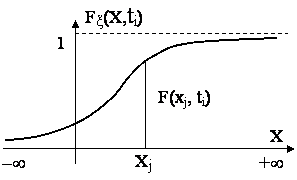Рис. 1.1. Функция распределения случайной величины (интегральный закон)

Для получения одной ординаты функции распределения, например  F(xj, ti) для x=xj (рис. 1.1) нужно подсчитать отношение числа раз n, когда значение ξ во всех N реализациях оказывались меньше или равными заданной величины xj, к общему числу N значений ξ, т.е. n/N. Это отношение называется частотой, а предел этого отношения при N®∞ называется вероятностью того, что случайная величина ξ будет меньше или равной величины xj, т.е. 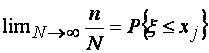. Очевидно, что если менять значения х, то и частота (вероятность) будет меняться, причем при х® -∞ Fξ(-∞,ti)=0, а при х®∞ Fξ(∞,ti) =1 (n=N), т.е. . Функция распределения является полным статистическим описанием случайной величины в том смысле, что по ней можно определить все возможные значения случайной величины и соответствующие им вероятности. Например, вероятность того, что случайная величина ξ находится в интервале {x1,x2}

Случайная величина ξ описывается также  плотностью распределения (дифференциальным законом)

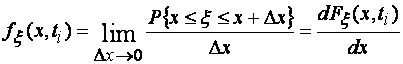             (1.2)

В качестве примера на рис. 1.2 показана функция fξ(x,ti). Имея N значений случайной величины можно построить ступенчатую функцию – гистограмму распределения случайной величины (ступенчатая функция на рис. 1.2). Для этого область изменения х разделяют на определенное число интервалов ∆х и каждому интервалу ставят в соответствие отношение n/N для этого интервала. При уменьшении интервала ∆х функция будет приближаться к непрерывной.

 


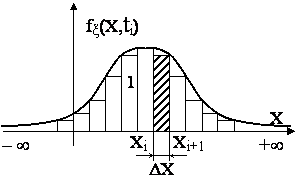
Рис. 1.2. Плотность распределения случайной

величины (дифференциальный закон)

Из (1.2) следует, что

 или

,

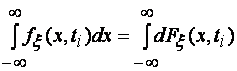
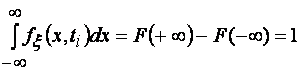т.е. площадь, ограниченная  функцией fξ(x,ti) и осью х равна 1. С помощью функции fξ(x,ti) можно приближенно подсчитать вероятность того, что в момент времени ti случайная величина ξ находится в интервале {x,x+∆x}:

 

(заштрихованная площадь на рис. 1.2).

Отметим, что случайные величины, функции распределения которых дифференцируемы по х при любых х, называются непрерывными.

В ряде случаев нет необходимости полного описания случайной величины ее функцией распределения. Большинство практических задач можно решать с помощью немногих усредненных характеристик распределения mn, образующихся из моментов ν порядка случайной величины ξ относительно числа а – т.е. математического ожидания случайной величины (ξ-а)ν.

Скачать файл