Информатика и выч. техника \ Основы информатики и вычислительной техники

Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 26

1.  Энтропия равна нулю, т.е. , в том крайнем случае, когда одно из чисел  равно 1, следовательно, остальные равны нулю. Это тот случай когда об опыте или величине все известно заранее, он имеет один исход, и результат не дает новую информацию.

2.  Энтропия максимальна, т.е. , когда все состояния системы равновероятны, т.е. . При этом ,                        (1.67)

т.е. соответствует оценке меры информации по Хартли (1.60), определяющей максимальное количество информации.

Следствия:

–  для равновероятных состояний энтропия есть монотонно возрастающая функция числа состояний.

Например, имеется 2 источника – табл. 1.5 а и б.

Х1

Х2

Х3

Х10

0,1

0,1

0,1

0,1

Х1

Х2

0,5

0,5

           а)                                            б)

Табл. 1.5

Для первого источника априори известно 50% исходов, а для второго – 10%, т.е. для первого источника возможности выбора (неопределенность) меньше, чем для второго.

-  энтропия есть вещественная ограниченная и неотрицательная функция, т.к. ,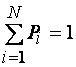  

-  всякое изменение вероятностей P1, P2,….PN в сторону их выравнивания увеличивает энтропию

-  Энтропия есть математическое ожидание логарифма вероятности, т.е. . Это выражение имеет такой же вид, как и выражение для энтропии, используемое в термодинамике и статистической механике.

Если энтропия источника раскрывается по этапам, то полная энтропия будет суммой  энтропий, полученных на каждом этапе.

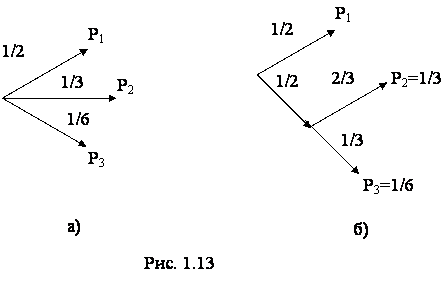Пример. Пусть имеется три события с вероятностями Р1=1/2, Р2=1/3, Р3=1/6. (рис 1.13). Энтропия будет .

Сначала делаем выбор между двумя возможными вероятностями, равными 1/2 и 1/2, а затем для второй возможности выбора делаем выбор между возможностями с вероятностями 2/3 и 1/3 от 1/2. Окончательно имеем те же вероятности, что и прежде.

В этом случае требуется, чтобы

Коэффициент 1/2 во втором члене суммы связан с тем, что выбор на втором этапе происходит только в половине общего числа случаев.

Рассмотрим вопрос о единицах измерения энтропии. В силу безразмерности вероятностей энтропия является безразмерной величиной. Однако для практических целей необходимо ввести единицу ее измерения.

За единицу измерения энтропии может быть принята энтропия любого объекта, для которого

Скачать файл