Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 29

Согласование осуществляется путем соответствующего кодирования сообщений. Если ко входу канала подключен источник сообщений с энтропией, равной пропускной способности канала связи, то считается, что источник согласован с каналом. Если энтропия источника меньше пропускной способности канала, что может быть в случае неравновероятности состояний источника, то источник не согласован с каналом, т.е. канал используется не полностью.

Согласование в статистическом смысле достигается с помощью статистического кодирования. Оно позволяет повысить энтропию передаваемых сообщений до величины, которая получается, если символы новой последовательности равновероятны. При этом число символов в последовательности будет сокращено. В результате источник информации согласуется с каналом связи.

При передачи информации через канал с помехами сообщения искажаются и на приемной стороне нет уверенности в том, что принято именно то сообщение, которое передавалось. Следовательно, сообщение недостоверно, вероятность правильности его после приема не равна единице. В этом случае количество получаемой информации уменьшается на величину неопределенности, вносимой помехами, т.е. вычисляется как разность энтропии сообщения до и после приема: , где Н(i) – энтропия источника сообщений;  - энтропия сообщения на приемной стороне.

Таким образом, скорость передачи по каналу связи с помехами

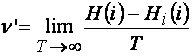                                                                          (1.70)

Пропускной способностью канала с шумами называется максимальная скорость передачи информации при условии, что канал связи без помех согласован с источником информации:

.

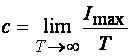Если энтропия источника информации не превышает пропускной способности канала (Нс), то существует код, обеспечивающий передачу информации через канал с помехами со сколь угодно малой частотой ошибок или сколь угодно малой недостоверностью. Пропускная способность канала связи при ограниченной средней мощности аналогового сигнала

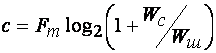,                                                           (1.71)

где F_m – полоса частот канала (Гц); W_c – средняя мощность сигнала; W_ш – средняя мощность шумов (равномерный спектр) с нормальным законом распределения амплитуд в полосе частот канала связи.

Следовательно, можно передавать информацию по каналу с помехами без ошибок, если скорость передачи информации меньше пропускной способности канала, определяемой формулой (1.71). Для скорости >c при любой системе кодирования частота ошибок принимает конечное значение, причем оно растет с увеличением значения. Из выражения (1.71) следует, что для канала с весьма высоким уровнем шумов (W_ш>>W_c) максимальная скорость передачи близка к нулю.

Подобно тому, как Хартлиевская мера информации используется для выбора одного состояния системы из ряда N равновероятных состояний, энтропия может быть использована для определения минимального количества двоичных вопросов необходимых для выбора (отгадывания) одного состояния системы из ряда N возможных неравновероятных состояний.

Энтропия  только при двух равновероятных значениях Р(0)=Р(1)=1/2, (в других случаях Н меньше одного бита и Н=0 при Р(0)=0, Р(1)=1 или Р(1)=1, Р₂=0). Следовательно, при ответе на двоичный вопрос количество информации зависит от того, какова вероятность получить утвердительный ответ, причем Р=1/2 соответствует максимуму информации. Отсюда следует практический вывод: если случайная величина ξ принимает значения с разными вероятностями, то при выборе (отгадывании) вопрос надо задавать так, чтобы вероятность ответа («да» или «нет») как можно меньше отличалась от 0,5; при этом ответ будет содержать наибольшее количество информации.