Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 13

 и т.д.

 

                            а)                                                      б)

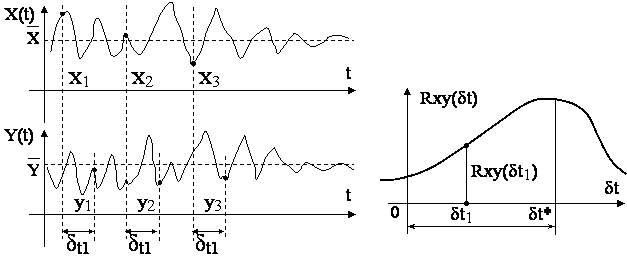
Рис. 1.7. Построение взаимной корреляционной функции R_XY (δt)

Аналогичным образом могут быть получены величины  для других значений  и в конечном счете – взаимная корреляционная функция  (рис. 1.7б)) Максимуму этой функции соответствует интересующий нас временной сдвиг, при котором действие значений x(t) (на входе системы) на значения y(t) (на выходе системы) проявляется с наибольшей статистической силой.

Значение  дает сдвиг по времени измерения значений y(t) по отношению к измерению значений x(t).

На рис. 1.8 показаны входной x(t) и выходной y(t) случайные сигналы, период дискретизации Т и сдвиг  между измерениями значений выходного и входного сигналов. Измеряемыми (дискретизируемыми) будут значения х₁, y₁; x₂, y₂; x₃, y₃ и т.д. .

При анализе случайных процессов наряду с корреляционными функциями широко применяются спектральные функции, которые характеризуют распределение энергии по частотным составляющим случайного сигнала. Наиболее широкое распространение среди таких функций получила спектральная плотность мощности , которая определяется, как производная по частоте от средней мощности (дисперсии) случайного процесса, определяемой выражением (1.14),

 

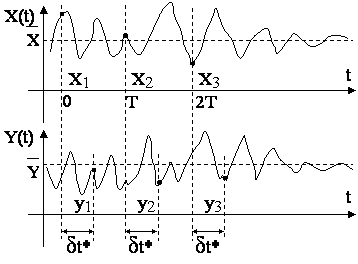
Рис 1.8. К определению измеряемых значений входного и выходного сигналов

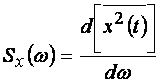                                                              (1.35)

Очевидно, что средней мощностью (средней интенсивностью, средним квадратом) процесса будет интеграл от спектральной плотности , т.е.

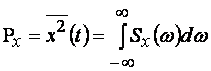                                                             (1.36)

Из определения (1.35) ясно, что функция  характеризует плотность, с которой дисперсии отдельных гармонии (частотных составляющих) случайного процесса распределяются по спектру частот. Например, теоретически возможен случайный сигнал с постоянной спектральной плотностью  в неограниченной полосе частот. Такой случайный сигнал называется белым или функциональным шумом. Реально такой сигнал создать нельзя. Поэтому практически ограничивают полосу частот, в пределах которых спектральную плотность можно считать постоянной. Практически считают, что если ширина частотного диапазона, в пределах которого спектральная плотность постоянна, по крайней мере на порядок больше полосы пропускания исследуемой системы, то этот источник для данной системы можно считать эквивалентом источника белого шума.

Спектральная плотность мощности  и корреляционная функция  для стационарного процесса, принимающего только действительные значения, связаны между собой прямым и обратным преобразованием Фурье

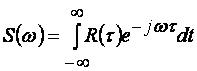                                                                 (1.37)