Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 12

В частном случае – независимых случайных сигналов х(t) и y(t) одномерная плотность вероятности  не зависит от значения  y(t_j) и

                             (1.28)

Нахождение одномерной плотностей вероятности (1.27) представляет собой достаточно сложную задачу. Еще более сложную задачу – нахождение двумерной и более плотности вероятности системы двух случайных сигналов. Поэтому на практике используются более простые, хотя и менее информативные, рассмотренные выше числовые характеристики случайных сигналов. Для оценки взаимной корреляции двух случайных сигналов x(t) и y(t) пользуются понятием взаимной корреляционной (кросскорреляционной) функции R_xy(τ), которая характеризует силу статистической связи случайных значений этих сигналов, отстоящих друг от друга на интервал τ.

По аналогии с (1.19), (1.20):

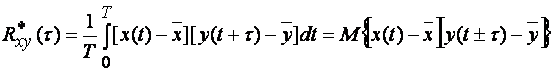  (1.29)

Или для центрированных сигналов x(t) и y(t)

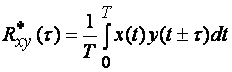                                      (1.30)

При t=0 максимальна и равна оценке взаимной дисперсии , т.е. .При  , что означает независимость значений сигналов x(t) и y(t).

Размерность  равна произведению размерностей x(t) и y(t), что неудобно при сравнении взаимных корреляционных функций двух пар случайных сигналов. Кроме того  характеризует не только статистическую связь x(t) и y(t) но и разброс значений этих сигналов относительно их математических ожиданий. Поэтому практически пользуются нормированной (безразмерной) взаимной корреляционной функцией:

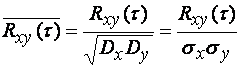                                    (1.31)

Очевидно, что  (при τ=0  при )

Отметим, что корреляционная функция R_z(t) случайного сигнала , являющегося суммой (разностью) двух стационарных сигналов x(t) и y(t)

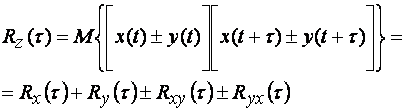             (1.32)

При этом математическое ожидание суммы (разности) случайных сигналов равно сумме (разности) их математических ожиданий. В случае независимых сигналов (взаимная корреляционная функция равна нулю) корреляционная функция

                                                                          (1.33)

При анализе информационных систем часто ставится задача определения периода измерения (дискретизации) Т входного x(t) и выходного y(t) случайного сигналов и определения времени сдвига δ_t^* измерений значений выходного сигнала по отношению к значениям входного сигнала.

Первая часть задачи решается путем нахождения интервалов корреляции  (для x(t)) и  (для y(t)), и выбору из них наибольшего, т.е. 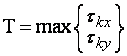                                                                               (1.34)

Вторая часть задачи решается путем построения взаимной корреляционной функции  .

Определение величины для одного значения временного сдвига, например для  (рис. 1.7а,б) практически осуществляется в соответствии с (1.29) путем вычисления среднего арифметического произведений