Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 24

Табл. 1.2

Предположим, что в результате приема M сигналов ί-тый символ повторяется К_i раз и каждый раз вносит информацию, количество которой оценивается как I_i . Тогда средняя информации, доставляемая в результате одного опыта

,                                       (1.62)

но количество информации от одного символа I_i связано с вероятностью его появления Р_i в соответствии с (1.61)

                                                                                  (1.63)

Тогда

или

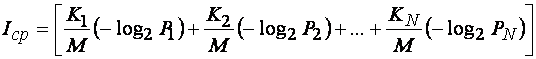      (1.64)

Отношения  представляют собой частоты повторения символов, а следовательно могут быть заменены их вероятностями, т.е. . Поэтому средняя информация в битах

                  (1.64)

или 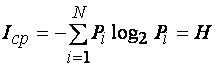                                                               (1.65)

Другими словами, если I_i – частное количество информации от одного символа (1.63), то среднее количество информации I_ср равно математическому ожиданию частных количеств информации, т.е.

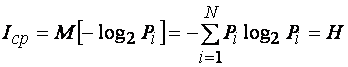
При равновероятных и независимых символах все P=1/N и формула (1.65) преобразуется в формулу Хартли (1.60).

Формулу (1.65) называют формулой Шеннона (по имени математика К. Шеннона). Величину H называют энтропией, которая является мерой неопределенности. Поясним смысл формулы Шеннона. Для этого рассмотрим серию опытов, в результате каждого из которых имеет место одно из несовместимых событий Х₁, Х₂, Х₃ …Х_N, образующих полную группу событий, для которой справедливо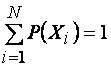

Для примера пусть число событий N=8, каждое событие содержит 3 символа и имеет вероятность Р_i (табл. 1.3)