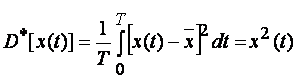Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 10

                         (1.18)

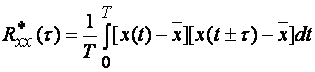                     (1.19)

или для центрированного сигнала

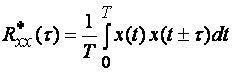                                      (1.20)

Выражение (1.17) определяет оценку математического ожидания – среднего значения случайного сигнала. Наиболее близким к нему, в случае сигнала, заданного N значениями х_i, является среднее арифметическое N значений случайного сигнала или выборочное среднее (рис. 1.3)

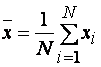                                                       (1.21)

 

Рис 1.3. Оценка математического ожидания случайного сигнала

Выражение (1.18) дает оценку дисперсии , которая характеризует разброс значений х_i от математического ожидания. Наиболее близким к нему в случае сигнала, заданного N значениями x_i, является среднее арифметическое квадратов N центрированных значений случайного сигнала или выборочная дисперсия

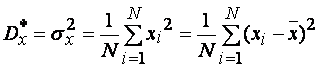           (1.22)

где - среднеквадратическое отклонение.

Выражение (1.19) дает оценку корреляционной функции. Практически, для нахождения одного ее значения например,  для , по одной реализации случайного сигнала х(t) (рис. 1.4а) нужно взять определенное количество произведений значений х(t), отстоящих друг от друга на величину , и найти их среднее арифметическое, т.е.

 

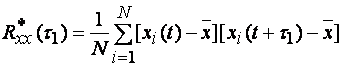
а)                                                     б)

Рис. 1.4. Построение корреляционной функции R_XX (τ), для значения τ=τ₁

Величина  (рис. 1.4б) показывает среднюю силу статистической связи случайных значений сигналов х₂ и х₁, х₄ и х₃, х₆ и х₅ и т.д., отстоящих друг от друга на интервал . Если величина  большая – то и сила связи большая (зная одно значение сигнала можно предсказать другое), если величина  мала – то и статистическая связь этих значений мала (зная одно значение сигнала, например х₁, трудно прогнозировать другое – х₂). Аналогичным образом могут быть определены значения корреляционной функции для других значений . Для автоматического измерения множества ординат автокорреляционной функций используются специальные приборы – коррелометры.

Из (1.19), (1.20) следует, что является четной функцией, т.е. = При   максимальна и равна оценке дисперсии, т.е. . С увеличением  статистическая связь между двумя значениями случайного сигнала ослабевает и при  .