Основы информатики и вычислительной техники: Учебно-практическое пособие, страница 21

                                                        Таблица 1.1

В общем случае, при числе символов S в алфавите и числе букв n в слове, число возможных слов

N=Sⁿ.                                                                  (1.53)

Число N называется комбинаторной мерой информации. Однако величина N неудобна для практической оценки информационной емкости, так как при заданном S количество информации растет экспоненциально с увеличином n - числом букв в слове, причем вклад каждого последующего значения  n нарастает.

         Для того, чтобы мера информации имела практическую ценность необходимо, чтобы количество информации I было пропорционально числу n, т.е. должно обеспечиваться соотношение:

I=Kn,                                                                                                        (1.54)

где K– постоянная, не зависящая от S.

         Допустим, что имеются две системы символов S₁ и S₂; им соответствует K₁ и K₂ такие, что если

,                                                       (1.55)

то и

I=K₁n₁=K₂n_2.                                                      (1.56)

         Из (1.55) и (1.56) следует, что

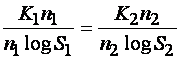  или 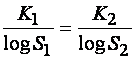 .                    (1.57)

         Это соотношение тождественно, если K=logs, т.е.

K₁=logS₁,                               (1.58)

 K₂=logS₂.

Подставив (1.58) в (1.54) и используя (1.53) получим:

I=nlogS=logSⁿ=logN,                                         (1.59)

т.е. в качестве меры информации I может быть принят логарифм числа возможных слов (состояний) N.

Рассмотрим насколько функция I отражает количественную оценку информации. Для этого должны выполняться 3 условия:

1.  Априори известно, что количество информации системы, имеющей одно состояние, равно 0. Действительно, в соответствии с (1.59) I=I(1)=log1=0, т.е. условие выполняется.

2.  Допустим, что физическая система состоит  из двух независимых систем и является их объединением.

Обозначим:

N; I – общее число состояний и количество информации всей системы соответственно;

N₁; I₁ – число состояний и количество информации первой системы;

N₂; I₂ – число состояний и количество информации второй системы.

     Очевидно, что N=N₁N₂ (одному состоянию первой системы соответствует N₂ состояний второй системы и т.д.) Общее количество информации I=I(N)=I(N₁N₂).Естественно считать, что суммарная информация должна быть равна сумме информации первой и второй системе, т.е. обладать свойством аддитивности, т.е. I(N₁N₂)=I(N₁)+I(N₂)

Действительно, в соответствии  с (1.59)

I=I(N)=logN=log(N₁N₂)=logN₁+logN₂, т.е. условие выполняется.

3.  Естественно потребовать, чтобы зависимость количества информации от числа состояний была монотонной, т.е. I(N₂) > I(N₁) при N₂>N₁. Действительно в соответствии с (1.59) I(N₂)=logN₂; I(N₁)=logN₁,  I(N₂)>I(N₁) при N₂>N₁.

Таким образом оценка меры информации I в соответствии с (1.59) удовлетворяет всем трем условиям.

Величина I называется хартлиевской (аддитивной) мерой информации по имени ученого Р.В.Л. Хартли, который, рассматривал процесс получения информации, как выбор одного сообщения (символа) из конечного наперед заданного множества N равновероятных и независимых сообщений, а количество информации I , содержащееся в выбранном сообщении, определял как двоичный логарифм N, т.е.