7. СТАЦИОНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ НА ПЛАСТИНЕ
В ГАЗОВОМ ПОТОКЕ
В данном разделе будет рассмотрена задача о продольном обтекании пластины потоком газа при достаточно больших числах Рейнольдса и любых числах Маха, для которых газ можно считать сплошной средой, а коэффициенты теплоемкости постоянными. Мы будем рассматривать некоторый гипотетический газ, для которого вязкость линейно зависит от температуры, а число Прандтля равно единице (впрочем, близкий по своим свойствам к воздуху, для которого m » T0,75, Pr = 0,72).
Обратимся к системе уравнений (4.14). Перепишем ее в безразмерном виде, сделав некоторые упрощения в связи с рассматриваемой задачей.
1. Положим dP/dx = 0.
2. Введем понятие энтальпии h = CpT и полной энтальпии h0 = h + u2/2.
3.
В качестве линейного размера вдоль x примем L; вдоль y - ![]() .
.
4.
За характерную скорость вдоль x возьмем V, вдоль y - ![]() .
.
5.
За масштаб давления выберем ![]() , а за масштаб
энтальпии –
, а за масштаб
энтальпии – ![]() .
.
6. Число Pr будем считать постоянным, т.е. m/m* = k/k*.
Тогда систему (4.14) можно записать в безразмерном виде:
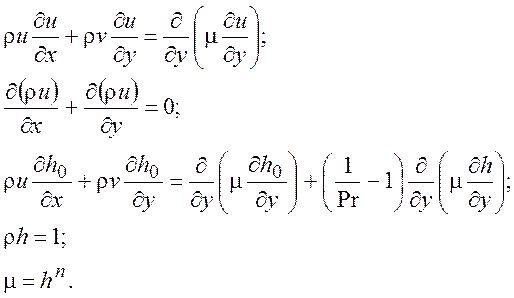 (7.1)
(7.1)
Граничные условия на скорость будут иметь вид
u(0) = v(0) = 0, u(¥) = 1.
Граничные условия на температуру могут быть двух родов:
а) задана энтальпия на поверхности
h(0) = hw, h(¥) = 1.
б) условие отсутствия теплоотдачи с поверхности пластины (теплоизолированная пластина)
![]() при y = 0, h(¥) = 1.
при y = 0, h(¥) = 1.
7.1. Распределение скорости
А.А. Дородницын (1942) указал общее преобразование координат, приводящее первые два уравнения системы (7.1) к форме, совпадающей с задачей Блазиуса. Это преобразование имеет вид
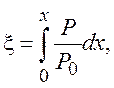
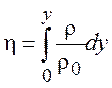 , (7.2)
, (7.2)
где P0 и r0 - параметры торможения (P и r в (7.2) размерные). Для плоской пластины вместо P0 и r0 возьмем их значения на границе пограничного слоя, тогда преобразования Дородницына будут иметь вид
![]() ,
, 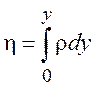 . (7.3)
. (7.3)
Перейдем в первом уравнении системы (7.1) к новым переменным с учетом уравнения состояния и закона для вязкости (последние два равенства в (7.1). Получим
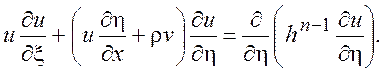 (7.4)
(7.4)
Уравнение неразрывности позволяет ввести функцию тока y, удовлетворяющую равенствам
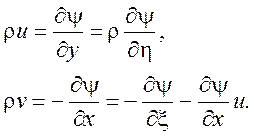 (7.5)
(7.5)
Обозначим
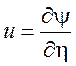 ;
; 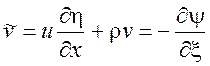 , (7.6)
, (7.6)
то есть u и ![]() удовлетворяют уравнению
неразрывности. Тогда для n = 1 из (7.4) и (7.6)
можно составить следующие уравнения:
удовлетворяют уравнению
неразрывности. Тогда для n = 1 из (7.4) и (7.6)
можно составить следующие уравнения:
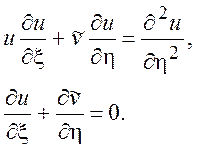 (7.7)
(7.7)
По форме записи уравнения (7.7) совпадают с задачей Блазиуса, т.е. в переменных (x, h) распределение скорости будет соответствовать уже решенной задаче об обтекании плоской пластины несжимаемым потоком.
7.2. Интеграл Крокко
Рассмотрим теперь уравнение энергии в системе (7.1). Для числа Pr = 1 оно примет вид
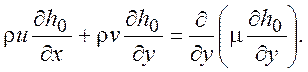 (7.8)
(7.8)
Уравнение (7.8) по форме записи совпадает с первым уравнением системы (7.1). Из этого следует существование очевидного частного интеграла
![]()
![]() (7.9)
(7.9)
Или, переходя к безразмерной температуре, получим
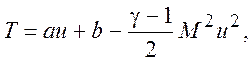 (7.10)
(7.10)
здесь М
– число Маха на границе пограничного слоя. Постоянные ![]() и
b определяются из граничных условий
и
b определяются из граничных условий
T(0) = Tw, T(¥) = 1. (7.11)
Подстановка констант в (7.10) дает квадратичную связь между температурой и скоростью, которая носит имя интеграла Крокко
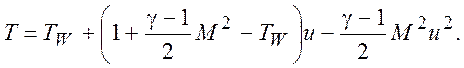 (7.12)
(7.12)
Для теплоизолированной поверхности должно выполняется условие ![]() при y = 0.
Из этого условия следует, что
при y = 0.
Из этого условия следует, что
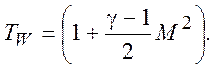 (7.13)
(7.13)
Для течения газа с Pr = 1 температура теплоизолированной поверхности равна температуре торможения. Хорошее приближение для реальных газов дает модифицированный интеграл Крокко
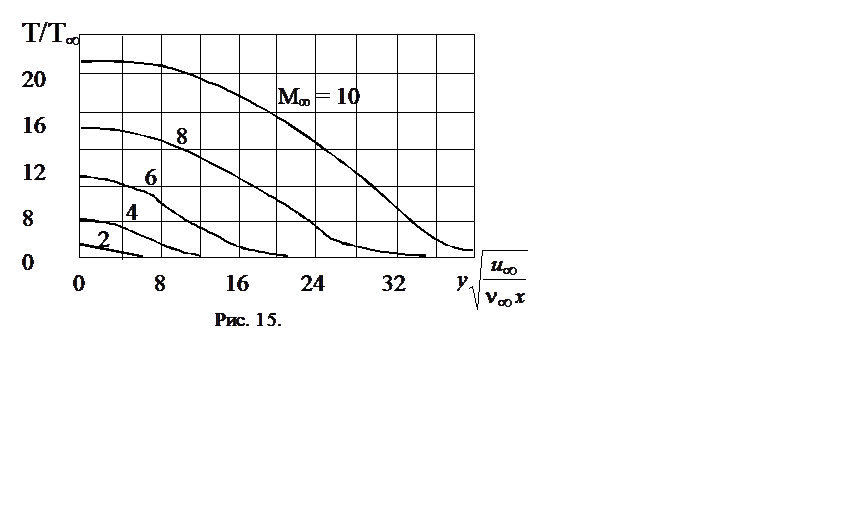
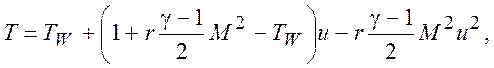 (7.14)
(7.14)
где r - коэффициент восстановления. Тогда температура теплоизолированной пластины в потоке реального газа будет
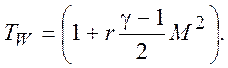 (7.15)
(7.15)
Для ламинарного течения ![]() (для турбулентного течения
(для турбулентного течения ![]() ).
).
Интеграл Крокко (7.12) и распределение скорости Блазиуса позволяет восстановить в физических переменных профили скорости и температуры в пограничном слое пластины для заданного числа Маха. Для этого сначала запишем распределение температуры в переменных Дородницына, подставив профиль Блазиуса u(h) в выражение (7.12). Мы получим распределение T(h). Затем вычисляем интеграл, который следует из (7.3)
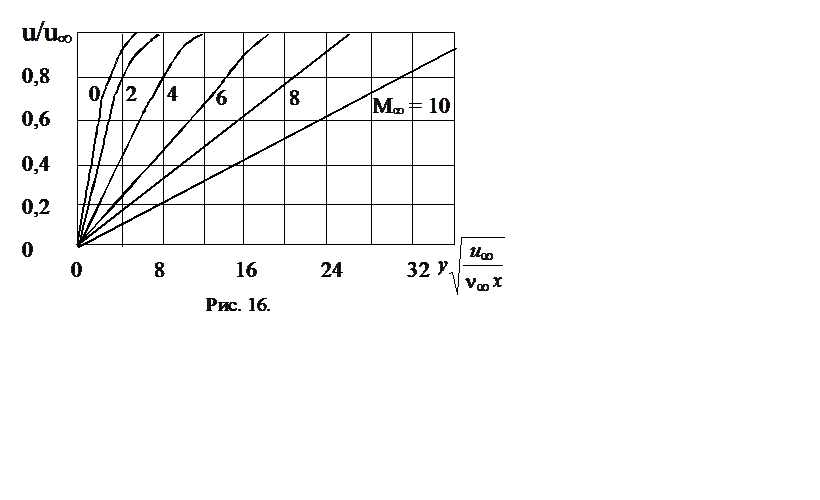
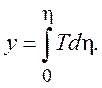 (7.16)
(7.16)
Результаты вычисления дают связь переменных y и h, что позволяет выразить скорость в зависимости от физической координаты y, а затем, опять используя (7.12), получить зависимость T(y).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.