Столкновительные процессы в плазме

Лекция № 3

Столкновительные процессы в плазме

          Как отмечалось в [1], принципиальным моментом в описании физико-химических процессов в плазме является определение сечения столкновения данного процесса.

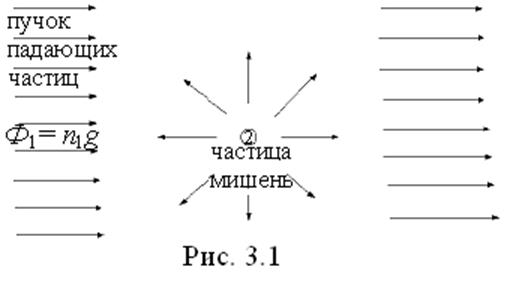          Рассмотрим однородный пучок падающих частиц, направленный на частицу-мишень (рис. (3.1). Пусть  - плотность падающих частиц пучка, а  - их скорость относительно частицы мишени. Тогда отношение числа падающих частиц, сталкивающихся с частицей-мишенью в единицу времени , к потоку частиц   определим как полное сечение столкновения

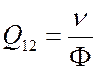                                     (3.1)

Полное сечение столкновения – это величина, характеризующая сталкивающиеся частицы (т.е. атомная величина), зависит только от типов взаимодействующих частиц и от относительной скорости  ().

 В данном выше определении полного сечения столкновения совершенно не говорится о типе столкновения. Это сечение равно сумме сечения упругого столкновения и сечений всех сопутствующих неупругих столкновений, т.е.

          .                                                                              (3.2)

          Каждое из этих конкретных сечений может быть определено аналогично (3.1) при соответствующей замене числителя. Например, если частица- мишень - атом в основном состоянии, то сечение возбуждения первого уровня частицы-мишени за счет воздействия на нее падающей частицы определится следующим соотношением:

          ,

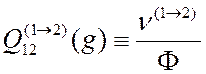где - число падающих частиц, вызывающих возбуждение  частицы-мишени в единицу времени. В данном случае . Если бы падающей частицей был электрон, то величина  равнялась бы нулю до тех пор, пока 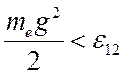. Заметим, что при малых  мы имеем, очевидно, . Когда же скорость  оказывается достаточно большой для осуществления неупругого столкновения, второе слагаемое в правой части равенства  (3.2) становится приблизительно того же порядка, что и .

          Вводится дифференциальное сечение рассеяния в телесном угле  (рис. 3.2):

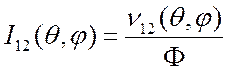          ,                                                                             (3.3)

где  - число падающих частиц, рассеиваемых частицей-мишенью в телесный угол  в единицу времени. Величина  фактически связана с соответствующим сечением соотношением

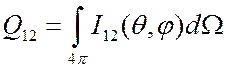                                       (3.4)

и зависит от конкретного типа взаимодействия  и от относительной скорости .

Так при упругом рассеянии будем иметь

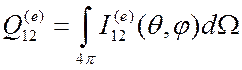          .                                                                            (3.5)

Величина

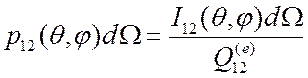                                                                   (3.6)

есть вероятность упругого рассеяния в элемент телесного угла

          Когда падающая частица упруго взаимодействует с неподвижной частицей-мишенью, она теряет импульс в направлении своего начального движения. Уменьшение z - компоненты импульса частиц в направлении  равно

,

т.к. для упругого рассеяния . Поскольку число падающих частиц, упруго рассеивающихся в телесном угле  в единицу времени равно , полное уменьшение z - компоненты импульса в единицу времени есть

  

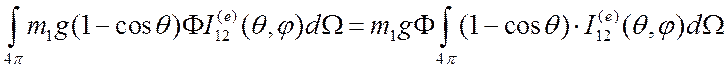
Величина  есть плотность потока импульса в пучке падающих частиц. Поэтому можно ввести величину

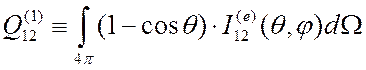                                                                     (3.7)

и назвать ее сечением передачи импульса.

          Определим среднюю долю импульса, теряемую падающей частицей при упругом столкновении:

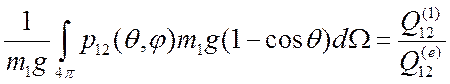          .                                              (3.8)

Сравним величины  и . Благодаря наличию в формуле (3.7) множителя

 рассеяние на большие углы дает больший вклад в сечение, чем рассеяние на малые (действительно,  при  и  при ). В случае упругого рассеяния электрона на атоме при достаточно малых энергиях , но при более высоких энергиях  может стать даже вдвое меньше . Полное сечение упругого рассеяния  не фигурирует в точной кинетической теории коэффициентов переноса газов (теплопроводности, вязкости, электропроводности). При вычислении коэффициентов переноса оказывается более предпочтительным использовать набор обобщенных сечений столкновений с передачей импульса, определяемых соотношением

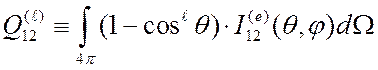          ,                                                        (3.9)

где  - целое число.

Для того чтобы при исследовании взаимодействия частиц в газе можно было пользоваться понятием сечения столкновения, необходимо предположить, что газ достаточно разрежен и длительность столкновения много меньше времени между двумя столкновениями. Далее, одну частицу будем считать частицей-мишенью, а остальные частицы можно рассматривать как входящие в состав пучков падающих частиц с бесконечно малой интенсивностью , движущихся к частице-мишени со всех сторон.  Для наглядности здесь будем считать скорости  относительного движения всех частиц газа приблизительно одинаковыми, тогда суммируя по всем бесконечно малым пучкам, получим, что число падающих частиц, взаимодействующих с частицей-мишенью в единицу времени, равно . Если в единице объема находится  частиц-мишеней, то полная скорость процесса (т.е. полное число столкновений в единицу времени между падающими частицами и частицами-мишенями на единицу объема) есть