Столкновительные процессы в плазме, страница 2

          .                                                                                 (3.10а)

Если падающие частицы и частицы-мишени идентичны, то в этой формуле каждое столкновение учитывается дважды, а поэтому .

 В более общем виде, для некоторого процесса

          .                                                                              (3.10б)

Полная частота столкновений падающей частицы со всеми частицами-мишенями определяется как

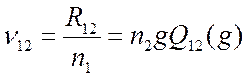          .                                                                           (3.11)

Частоты  столкновений для отдельных процессов определяются аналогичным образом:

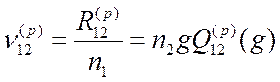          .                                                                      (3.12)

Примером может служить частота столкновений с передачей импульса

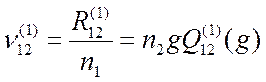          .                                                                        (3.13)

          Теперь перейдем к общему случаю, когда относительные скорости частиц газа меняются произвольным образом. Рассмотрим простейшую модель однокомпонентного частично ионизованного газа содержащего три типа частиц - электроны, положительные ионы и нейтральные частицы. Приближенные результаты для более сложных газов, содержащих несколько ионных и нейтральных компонент, могут быть получены с помощью простой модели, если ее параметры интерпретировать как определенным образом усредненные параметры ионной и нейтральной компонент сложной реальной системы.

Средняя скорость каждой компоненты плазмы по отношению к некоторой  лабораторной системе координат определяется выражением

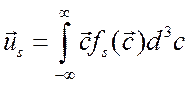          ,                                                                                   (3.14)

где  - функция распределения по скоростям компоненты  .

          В общем случае величина  есть функция координат и времени.

Удельные плотности электронов, ионов и нейтральных частиц определяются следующими соотношениями:

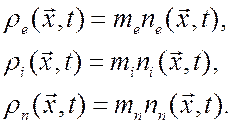                                                                                        (3.15)

Полная плотность газа равна

          .                                                                            (3.16)

Средняя массовая скорость газа определяется соотношением

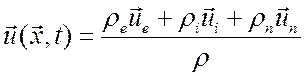          .                                                                   (3.17)

          Вообще говоря, скорости компонент газа могут отличаться от средне массовой скорости и одна от другой. Это различие удобно характеризовать диффузионной скоростью каждой компоненты:

          .                                                                     (3.18)

Из определения массовой скорости следует, что диффузионные скорости должны удовлетворять соотношению

          .                                                                         (3.19)

При описании столкновительных газов удобнее оперировать со скоростями частиц, измеренными в системе координат, движущейся со средней массовой скоростью , а не в лабораторной системе координат. Для этой цели вводится так называемая хаотическая скорость

          .                                                                                       (3.19a)

Выражение для диффузионной скорости компоненты  будет аналогично выражению (3.14):

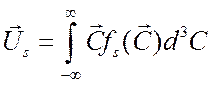          .                                                                                (3.19b)

Для простого газа  (т.е. газа, состоящего из одной компоненты)  . Результаты, выраженные через среднюю массовую скорость, в известном смысле соответствуют отклонениям первого порядка от того, что мы имеем в случае неподвижного газа.