Столкновительные процессы в плазме, страница 3

          Если каждая частица компоненты  несет заряд , то можно говорить о потоке плотности заряда, переносимого данной компонентой (в некоторой лабораторной системе координат); он называется плотностью тока компоненты и дается выражением

          .                                                                                             (3.20)

Вводя диффузионную скорость компоненты  и произведя подстановку

 можно написать

          ,                                                                                       (3.21)

где

                                                                                                       (3.22)

есть плотность тока проводимости данной компоненты,  - плотность конвекционного тока данной компоненты. В противоположность конвекционному току ток проводимости не зависит от системы отсчета. Полная плотность тока для всего газа получается суммированием по всем компонентам, 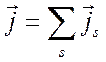 и может быть записана как

          ,                                                                                           (3.23)

где

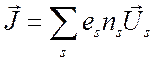                                                                                                    (3.24)

- плотность полного тока проводимости, а величина

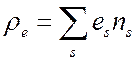                                                                                                     (3.25)

- полная плотность заряда. Если обозначим заряд, переносимый электроном, через  и предположим, что зарядовое  число иона  (заряд иона ), то в этом случае

                                                                                           (3.26)

и

          .                                                                                       (3.27)

          Теперь вновь обратимся к определению скорости процесса. В системе координат, движущейся с массовой скоростью, плотность падающих частиц в пучке бесконечно малой интенсивности равна . Скорость каждой такой падающей частицы относительно частицы-мишени со скоростью  равна . Следовательно, число частиц пучка, пересекающих в единицу времени единичную площадку, перпендикулярную вектору , равно , где

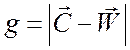 .                                                                                           (3.28)

Тогда для пучка, имеющего то же направление, что и вектор относительной скорости , дифференциальная плотность потока может быть записана следующим образом:

,                                                                              (3.29)

а дифференциальная скорость процесса р, определяется соотношением

          .                                           (3.30)

Полная скорость процесса  есть

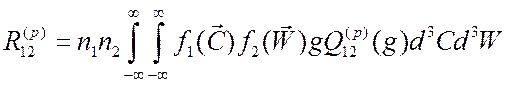          .                                      (3.31)

          Интеграл в уравнении (3.31) есть среднее значение величины . В случае процессов имеющих пороговую энергию, область интегрирования уменьшается и сводится к той области, где . В случае идентичности падающих частиц и частиц-мишеней в правой части равенства (3.31) добавляется множитель ½.

          Если  и  - максвелловские функции то скорость процесса р может быть записана следующим образом

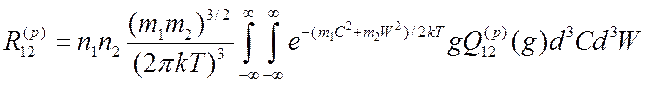          .                    (3.32)

Произведем замену переменных интегрирования, введя скорости центра масс и относительные скорости частиц:

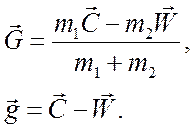                                                                                              (3.33)

Обратное преобразование имеет вид

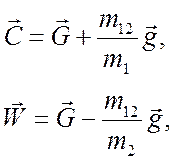                                                                                                (3.34)

где 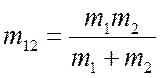 - приведенная масса.

В новых переменных в сферической системе координат выражение (3.32) запишется:

         

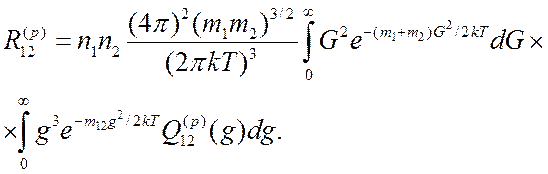
Поскольку 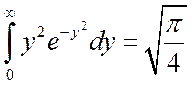, имеем окончательно

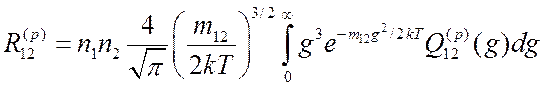          .                                 (3.35)