Лекция №2
 Рассмотрим один из наиболее интересных феноменов
газовой динамики, связанный с распространением волн сжатия – ударной волны (УВ)
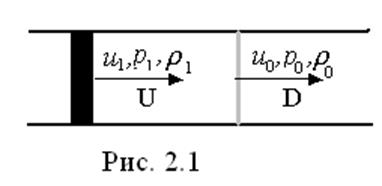
Представим себе систему, состоящую из цилиндра, заполненного газом, и поршня,
который постепенно, ускоряясь от состояния покоя вдвигаться в цилиндр со
скоростью U (рис. 2.1).Параметры невозмущенного состояния газа
обозначены индексом «0» возмущенного – «1», D - скорость
распространения УВ. Поршень генерирует характеристики С+,
граничная характеристика С0, соответствующая распространению фронта
волны сжатия со скоростью
Рассмотрим один из наиболее интересных феноменов
газовой динамики, связанный с распространением волн сжатия – ударной волны (УВ)
Представим себе систему, состоящую из цилиндра, заполненного газом, и поршня,
который постепенно, ускоряясь от состояния покоя вдвигаться в цилиндр со
скоростью U (рис. 2.1).Параметры невозмущенного состояния газа
обозначены индексом «0» возмущенного – «1», D - скорость
распространения УВ. Поршень генерирует характеристики С+,
граничная характеристика С0, соответствующая распространению фронта
волны сжатия со скоростью ![]() , отделяет область покоя
от области движения. В следующий момент времени «возмущение», генерируемое
поршнем, начинает распространяться по возмущенному газу, в котором р и Т
выше чем в исходном со стоянии, а поскольку возмущение распространяется с
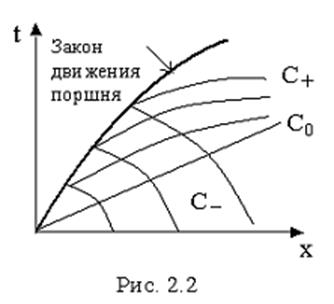
местной скоростью звука оно начнет догонять начальное возмущение. На графике t, х
(рис. 2.2) характеристики начнут сходиться.
, отделяет область покоя
от области движения. В следующий момент времени «возмущение», генерируемое
поршнем, начинает распространяться по возмущенному газу, в котором р и Т
выше чем в исходном со стоянии, а поскольку возмущение распространяется с
местной скоростью звука оно начнет догонять начальное возмущение. На графике t, х
(рис. 2.2) характеристики начнут сходиться.
 На характеристиках С- будет
сохраняться инвариант Римана J-, для которого
На характеристиках С- будет
сохраняться инвариант Римана J-, для которого 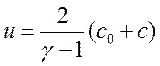 , и
видно, что скорость частиц на некотором расстоянии от фронта волны сжатия будет
выше чем, частиц примыкающих к фронту, т.е. газ будет поджиматься и появляется
тенденция к т.н. опрокидыванию волны, когда «хвост» волны начнет обгонять
«голову», что, очевидно, физически бессмысленно. Начиная с некоторого момента
времени С+ характеристики пересекутся, что приводит к неоднозначности
математического описания процесса. Единственным способом устранить возникающие
физические и математические противоречия является введение разрыва – ударной
волны, на котором естественно должны выполняться все физические законы
сохранения. Рассмотрим движение газа в системе координат, где ударная волна
покоится. Обозначим индексом «0» параметры газа, втекающего в разрыв, а
индексом «1», соответственно, вытекающего из него. Выпишем законы сохранения
потоков массы, импульса и энергии через поверхность разрыва:
, и
видно, что скорость частиц на некотором расстоянии от фронта волны сжатия будет
выше чем, частиц примыкающих к фронту, т.е. газ будет поджиматься и появляется
тенденция к т.н. опрокидыванию волны, когда «хвост» волны начнет обгонять
«голову», что, очевидно, физически бессмысленно. Начиная с некоторого момента
времени С+ характеристики пересекутся, что приводит к неоднозначности
математического описания процесса. Единственным способом устранить возникающие
физические и математические противоречия является введение разрыва – ударной
волны, на котором естественно должны выполняться все физические законы
сохранения. Рассмотрим движение газа в системе координат, где ударная волна
покоится. Обозначим индексом «0» параметры газа, втекающего в разрыв, а
индексом «1», соответственно, вытекающего из него. Выпишем законы сохранения
потоков массы, импульса и энергии через поверхность разрыва:
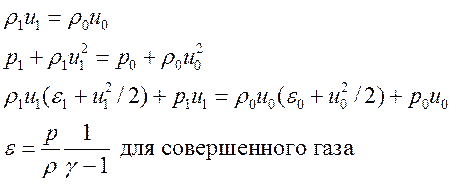 (2.1)
(2.1)
Формально соотношения (2.1) можно получить из исходной системы дифференциальных уравнений, которые являются выражением тех же законов сохранения:
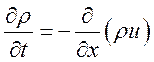
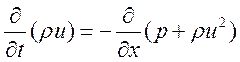 (2.2)
(2.2)
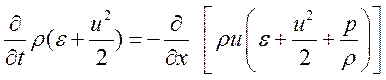
Будем сначала формально рассматривать разрыв как тонкий слой с большими градиентами всех величин и проинтегрируем уравнения по этому слою от х0 до х1. Например,
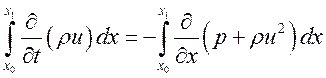 ®
® ![]()
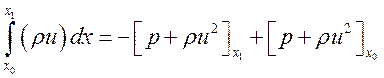
![]()
![]() Совершим предельный
переход, устремив толщину слоя к нулю
Совершим предельный
переход, устремив толщину слоя к нулю ![]() .
Интегралы в левых частях пропорциональные
.
Интегралы в левых частях пропорциональные ![]() исчезают
(что и соответствует отсутствию накопления массы, импульса и энергии в
разрыве), а правые части дают разности потоков соответствующих величин по обе
стороны разрыва, т.е. уравнение (2.1).
исчезают
(что и соответствует отсутствию накопления массы, импульса и энергии в
разрыве), а правые части дают разности потоков соответствующих величин по обе
стороны разрыва, т.е. уравнение (2.1).
Проделанный формализм указывает на то, что система уравнений (2.2) допускает разрывные решения, но из них невозможно получить структуру конечного разрыва без включения в (2.2) диссипативных факторов (таких как вязкость и теплопроводность).
Из системы (2.1) путем несложных преобразований следуют соотношения, связывающие параметры потока по обе стороны УВ.
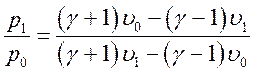 ;
; 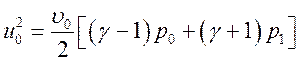 ;
;
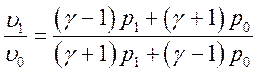 ;
; 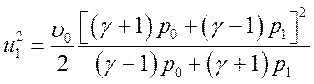 (2.3),
(2.3),
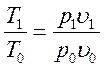
где ![]() - удельный объем.
- удельный объем.
В
неподвижной системе координат, где разрыв движется по неподвижному газу,![]() скорость УВ
скорость УВ ![]()
![]() а скорость газа за УВ
а скорость газа за УВ ![]()
Для
сильной ударной волны (![]() ) из (2.3) следует
) из (2.3) следует
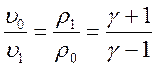 =
= 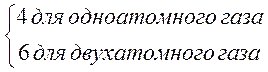 (2.4),
(2.4),
![]() =
= 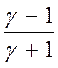
![]() >> 1 (2.5),
>> 1 (2.5),
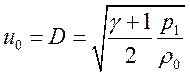
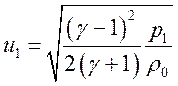 (2.6).
(2.6).
Определим числа Маха перед и за УВ
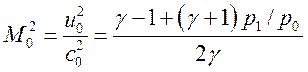 , (2.7),
, (2.7),
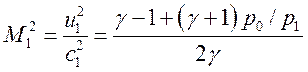 (2.8).
(2.8).
где с
- местная скорость звука, ![]() - показатель адиабаты. М0 еще называют
Махом ударной волны т.к.
- показатель адиабаты. М0 еще называют
Махом ударной волны т.к. ![]() .
.
Выразим через числа Маха перепады давления и плотности на УВ
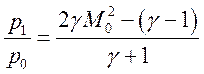 ;
; 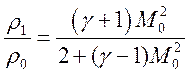 (2.9).
(2.9).
Для
сильной УВ ![]()
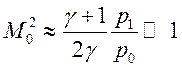
Для
слабой УВ, когда ![]()
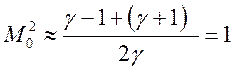 и
и ![]() т.е. слабые УВ движутся по
неподвижному газу со скоростью звука. Поскольку в УВ р1>р0 то М0>1,
т.е. слабые УВ движутся по
неподвижному газу со скоростью звука. Поскольку в УВ р1>р0 то М0>1, ![]() и газ
втекает в разрыв со сверхзвуковой скоростью, а вытекает из него с дозвуковой
скоростью
и газ
втекает в разрыв со сверхзвуковой скоростью, а вытекает из него с дозвуковой
скоростью ![]()
![]() Выпишем еще одно
полезное соотношение – отношение температур через Мах УВ
Выпишем еще одно
полезное соотношение – отношение температур через Мах УВ
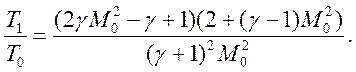 (2.10).
(2.10).
Для сильной УВ из (2.10) получим
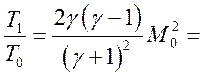
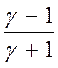
![]() (2.11).
(2.11).
 Изобразим
на диаграмме
Изобразим
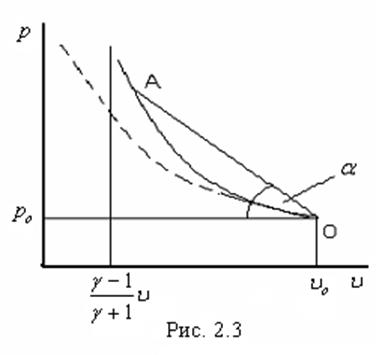
на диаграмме ![]() зависимость
зависимость ![]() ,
которая получила название ударной адиабаты (рис. 2.3). Пусть начальное состояние перед УВ
задается точкой
,
которая получила название ударной адиабаты (рис. 2.3). Пусть начальное состояние перед УВ
задается точкой ![]() , тогда возможные конечные
состояния будут определятся кривой, задаваемой выражением (2.3). Эта кривая,
согласно (2.4), должна иметь асимптоту
, тогда возможные конечные
состояния будут определятся кривой, задаваемой выражением (2.3). Эта кривая,
согласно (2.4), должна иметь асимптоту 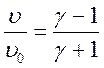 .
Проведем из начального состояния прямую ОА, пересекающую кривую конечных
состояний в некоторой точке
.
Проведем из начального состояния прямую ОА, пересекающую кривую конечных
состояний в некоторой точке ![]() . Наклон линии ОА к оси
. Наклон линии ОА к оси ![]() есть
есть 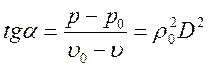 , откуда следует, что наклон прямой
ОА однозначно определяет скорость ударной волны. Для слабых ударных волн
, откуда следует, что наклон прямой
ОА однозначно определяет скорость ударной волны. Для слабых ударных волн 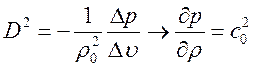 , т.е. адиабата Пуассона и ударная адиабата
имеют в точке О общую касательную. На рис. 2.3 адиабата Пуассона представлена
пунктирной линией.
, т.е. адиабата Пуассона и ударная адиабата
имеют в точке О общую касательную. На рис. 2.3 адиабата Пуассона представлена
пунктирной линией.
Отметим
одну интересную особенность течения с УВ. По обе стороны от нее течение
адиабатично и ![]() , а на разрыве вместо адиабаты –
ударная адиабата, т.е. на разрыве должен иметь место скачок энтропии. Определим
изменение энтропии на УВ. Запишем первое начало термодинамики для идеального
газа
, а на разрыве вместо адиабаты –
ударная адиабата, т.е. на разрыве должен иметь место скачок энтропии. Определим
изменение энтропии на УВ. Запишем первое начало термодинамики для идеального
газа ![]() и проинтегрируем его, воспользовавшись
уравнением состояния
и проинтегрируем его, воспользовавшись
уравнением состояния ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.