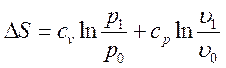 . (2.12)
. (2.12)
Подставляя
в (2.12) выражение ![]() и
и ![]() =
= ![]() через М02
из (2.9) получим
через М02
из (2.9) получим
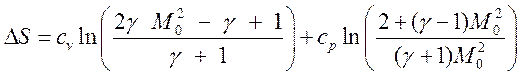 (2.13)
(2.13)
Рассмотрим
случай «слабых» ударных волн, т.е. М0 ~ 1. Представим ![]() , где d - малая величина из (2.13) будем иметь:
, где d - малая величина из (2.13) будем иметь:
![]()
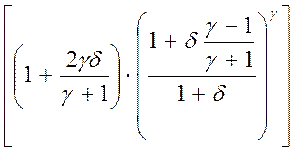
Разложим
логарифм по малой величине d с точностью до третьего порядка малости: ln(1+х) = х - ![]() +
+ ![]() и в результате получим
и в результате получим
![]()
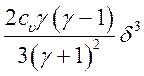 . (2.14).
. (2.14).
Выражение (2.14) можно представить в более привычном виде через перепад давления или плотности на УВ. Из (2.9)
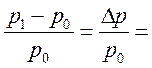
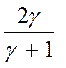 (М02
– 1) =
(М02
– 1) = 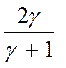 d, аналогично
d, аналогично 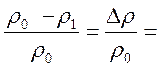
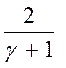 d и (2.14) запишется:
d и (2.14) запишется:
![]()
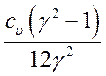
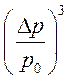 =
= 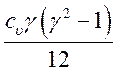
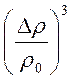 (2.15).
(2.15).
Из
(2.15) видно, что энтропия растет только в волнах сжатия ![]() , а существование ударных волн разрежения
невозможно: при
, а существование ударных волн разрежения
невозможно: при ![]() и Dr<0 DS<0, что термодинамически невозможно. Как мы уже
видели, для невязкого и нетеплопроводного газа ударная волна представляет
собой разрыв. Наличие вязкости и теплопроводности приводит к размазыванию УВ.
Оценим эффективную «толщину» ударного перехода, для плоской стационарной УВ.
и Dr<0 DS<0, что термодинамически невозможно. Как мы уже
видели, для невязкого и нетеплопроводного газа ударная волна представляет
собой разрыв. Наличие вязкости и теплопроводности приводит к размазыванию УВ.
Оценим эффективную «толщину» ударного перехода, для плоской стационарной УВ.
Исходная система уравнений есть:
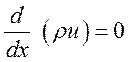 (2.16),
(2.16),
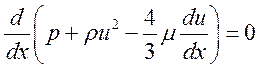 (2.17),
(2.17),
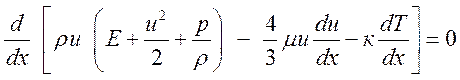 (2.18).
(2.18).
Рассмотрим уравнение импульсов (2.17) при m = соnst
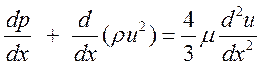 , откуда следует оценка
, откуда следует оценка
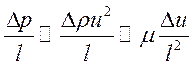 . (2.19)
. (2.19)
Пусть
УВ бежит с постоянной скоростью по неподвижному газу тогда ![]() и из (2.19) имеем l ~
и из (2.19) имеем l ~ 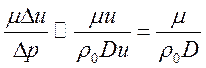 откуда для
откуда для 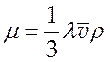 (l - длина свободного пробега,
(l - длина свободного пробега, ![]() - средняя скорость теплового
движения молекул) и с учетом того, что для сильной УВ
- средняя скорость теплового
движения молекул) и с учетом того, что для сильной УВ 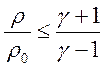 , а
, а ![]() ~ с = D получим
~ с = D получим
l~ l, (2.20),
т.е.
толщина фронта УВ сравнима с длиной пробега молекул. Поскольку коэффициент
теплопроводности 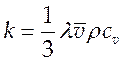 и
и ![]() , (что отображает общую природу явлений вязкости и
теплопроводности) то очевидно результат «размазывания» УВ за счет
теплопроводности будет того же порядка, что и за счет вязкости. На уровне
оценок это можно непосредственно получить из уравнения энергии, если пренебречь
в нем вязким членом.
, (что отображает общую природу явлений вязкости и
теплопроводности) то очевидно результат «размазывания» УВ за счет
теплопроводности будет того же порядка, что и за счет вязкости. На уровне
оценок это можно непосредственно получить из уравнения энергии, если пренебречь
в нем вязким членом.
Используем
полученные результаты для решения одной практически интересной задачи,
связанной с распадом произвольного разрыва. Рассмотрим трубу, разделенную
перегородкой и каждая половина заполнена разными газами, находящимися при
различных давлениях ![]() . В начальный момент перегородка
мгновенно убирается. Из самых общих соображений видно, что вправо будет
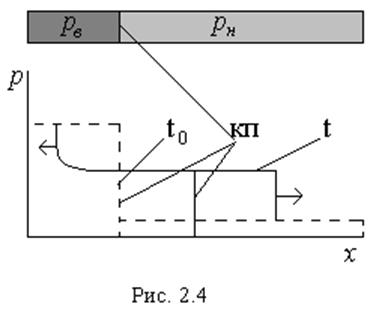
распространяться ударная волна, а влево волна разрежения. Условная диаграмма процесса
в переменных р, х представлена на рис. 2.4. Здесь
. В начальный момент перегородка
мгновенно убирается. Из самых общих соображений видно, что вправо будет
распространяться ударная волна, а влево волна разрежения. Условная диаграмма процесса
в переменных р, х представлена на рис. 2.4. Здесь ![]() – давление в камере высокого давления
и соответственно
– давление в камере высокого давления
и соответственно ![]() – низкого,
– низкого, ![]() начальный момент времени,
начальный момент времени, ![]() некоторый текущий момент времени, кп -
контактная поверхность.
некоторый текущий момент времени, кп -
контактная поверхность.
 Для
простоты предположим, что возникающая ударная волна сильная
Для
простоты предположим, что возникающая ударная волна сильная ![]() . Очевидно, что в начальный момент этому
условию будет соответствовать
. Очевидно, что в начальный момент этому
условию будет соответствовать ![]() . В этом приближении
можно считать, что газ в волне разрежения истекает в вакуум и скорость
истечения равна максимальной скорости:
. В этом приближении
можно считать, что газ в волне разрежения истекает в вакуум и скорость
истечения равна максимальной скорости:
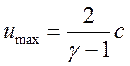 (2.21).
(2.21).
В силу
непрерывности течения поток газа в волне разрежения на контактной поверхности
должен непрерывно «смыкаться» с потоком газа за фронтом УВ, которую также будем
считать сильной. Тогда из (2.6) следует выражение для скорости УВ через
скорость потока за фронтом УВ 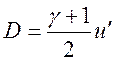 и после подстановки
туда
и после подстановки
туда ![]() получаем окончательно для скорости ударной
волны
получаем окончательно для скорости ударной
волны
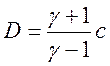 (2.22),
(2.22),
где
скорость звука 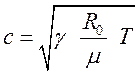 .
.
Рассмотренная
нами система называется ударной трубой. Совершенно очевидно, что для получения
больших скоростей ударных волн, создаваемых таким способом, в качестве
толкающего газа (область высокого давления) нужно выбирать легкий или (и)
сильно нагретый газ, что обеспечивало бы большую скорость звука, (например
водород, гелий). С другой стороны, при фиксированной скорости «толкающего» газа
наибольшие числа Маха У.В. будут получены в тяжелых газах, имеющих относительно
малую скорость звука. Если толкающий газ высокого давления водород (с = 1300
м/с), а газ низкого давления – воздух (с = 340 м/с), то максимальный Мах УВ ![]() и температура за фронтом УВ составит » 30000 К (без учета потерь на диссоциацию,
ионизацию и излучение), реально же она составит ~ 13000 К. Таким образом предельные оценки указывают на
возможность получения в схеме распада произвольного разрыва УВ с очень высокой
температурой газа за фронтом. Этот принцип послужил, как я уже сказал, основой
создания установок для получения ударных волн – ударных труб. Они получили
широкое распространение как простой способ исследований физико-химических
свойств различных веществ (уравнений состояния, спектральных характеристик,
переносных коэффициентов (теплопроводности, вязкости, проводимости) и т.п., а
так же как метод изучения механизма и определения многих неравновесных
молекулярных процессов в физической и химической кинетике. Кроме того, ударные
трубы используются в качестве импульсных аэродинамических труб для исследования
сверхзвукового обтекания различных тел высокотемпературным потоком газа.
и температура за фронтом УВ составит » 30000 К (без учета потерь на диссоциацию,
ионизацию и излучение), реально же она составит ~ 13000 К. Таким образом предельные оценки указывают на
возможность получения в схеме распада произвольного разрыва УВ с очень высокой
температурой газа за фронтом. Этот принцип послужил, как я уже сказал, основой
создания установок для получения ударных волн – ударных труб. Они получили
широкое распространение как простой способ исследований физико-химических
свойств различных веществ (уравнений состояния, спектральных характеристик,
переносных коэффициентов (теплопроводности, вязкости, проводимости) и т.п., а
так же как метод изучения механизма и определения многих неравновесных
молекулярных процессов в физической и химической кинетике. Кроме того, ударные
трубы используются в качестве импульсных аэродинамических труб для исследования
сверхзвукового обтекания различных тел высокотемпературным потоком газа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.