Уточнение моделей переноса. Диффузия в смеси двух газов. Теплопроводность

Лекция № 6

Уточнение моделей переноса.

          Процессы переноса, рассмотренные нами на основе элементарной кинетической теории, изучались в «чистом виде», то есть предполагалось отсутствие потоков не связанных с данным процессом. В действительности процессы переноса взаимосвязаны, например, при наличии диффузионных потоков всегда имеются тепловые потоки и наоборот.

Диффузия в смеси двух газов.

          Рассмотрим процесс диффузии в смеси двух газов с плотностями и , имеющих одинаковую температуру Т. Давление газа будем считать постоянным. Тогда вместе с изменением плотности будет меняться температура и средняя скорость частиц каждого сорта:

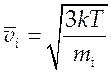,   i=1, 2                                                                                 (6.1).

Как и ранее, полный поток частиц сорта «i» через площадку dS будет равен разности односторонних потоков:

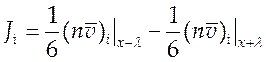                                                                         (6.2),

где односторонние потоки есть

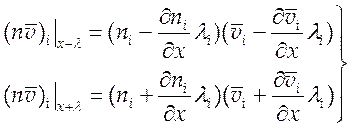                                                             (6.3).

Подставляя (6.3) в (6.2), с точность до малых первого порядка получим:

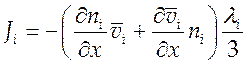                                                                            (6.4).

Скорость i-той компоненты газа определим как , и для относительной скорости компонент газа или скорости  диффузии согласно (6.4) будем иметь:

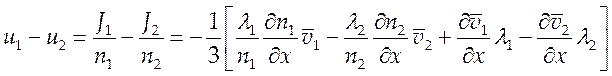                        (6.5).

          Обозначим  - безразмерная концентрация  i-той компоненты смеси, тогда парциальное давление можно записать

                                                                              (6.6).

Дифференцируя (6.6) по х при ,получим:

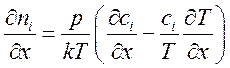                                                                              (6.7).

Подставим (6.7) в (6.5) и с учетом выражения для средней скорости (6.1) найдем скорость взаимной диффузии

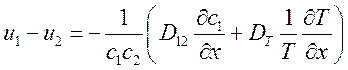                                                             (6.8),

где

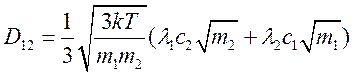                                                            (6.9)

--коэффициент взаимной диффузии

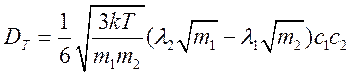                                                                       (6.10)

--коэффициент термодиффузии. При выводе (6.9) и (6.10) было учтено, что 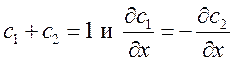. Средние длины свободного пробега определяются по формулам (4.20)

.

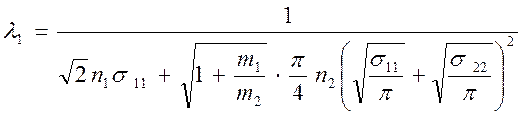
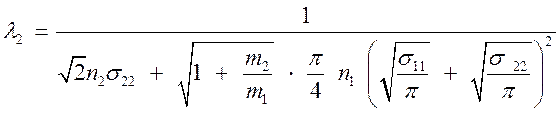Видно, что в общем случае  длины пробега  различны. Если , то более тяжелые молекулы диффундируют в холодную область. Если массы  молекул равны, то в холодную область диффундируют молекулы с большим сечением столкновения. Если массы молекул равны и , то термодиффузия отсутствует. Коэффициент взаимной диффузии обратно пропорционален давлению.

Теплопроводность.

Будем рассматривать газ, состоящий из молекул, атомов, ионов и электронов (это может быть моно газ или смесь различных газов).

Процесс переноса тепла может происходить как за счет кондуктивной теплопроводности (в отсутствие потоков массы – ), так и за счет диффузионных потоков массы при постоянном давлении. Рассмотрим вклад последней составляющей в тепловой поток.

Определим скорость газа как скорость центра тяжести системы

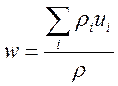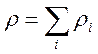;                                                                               (6.11),

где  - плотности смеси и ее компонент;  - скорости компонент смеси. Потоки массы отдельных компонент смеси относительно центра тяжести выражаются как

                                                                                                    (6.12).

Сумма этих потоков должна по определению равняться нулю

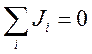                                                                                                            (6.13).

Рассмотрим в начале газ, состоящий из атомов и двухатомных молекул одного вещества при наличии диссоциации, но без учета ионизации. Тогда из (6.12) и (6.13) имеем

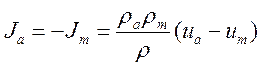                                                                          (6.14)

Подставим в (6.14) выражение (6.8) для разности скоростей, где производную от концентрации представим, как 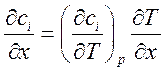 и в результате получим

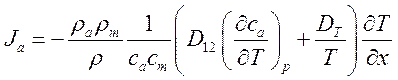                                                      (6.15).

Одним граммом смеси атомов и молекул переносится энтальпия:

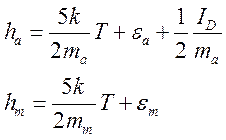                                                                                         (6.16),

здесь  - теплоемкость при постоянном давлении поступательных степеней свободы,  - энергия возбуждения электронов в атоме,  - энергия возбуждения вращательных и колебательных уровней,  - потенциал диссоциации. Потоком  переносится количество тепла, равное избыточной энергии, возникающей в процессе реакции преобразования единицы массы и равной 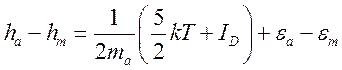. Таким образом, поток тепла , связанный с наличием потока массы (с учетом, что ) есть

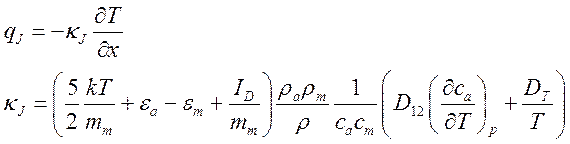                                        (6.17).

Полное количество переносимого тепла с учетом кондуктивной теплопроводности  составит

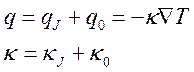                                                                                   (6.18).