Уточнение моделей переноса. Диффузия в смеси двух газов. Теплопроводность, страница 2

Коэффициент кондуктивной теплопроводности (в отсутствии потоков)  определяется как сумма коэффициентов теплопроводностей всех компонентов смеси

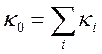                                                                                                 (6.19).

В практических расчетах кондуктивная теплопроводность компоненты «i» определяется по формулам элементарной кинетической теории с поправками, полученными на основе более строгой кинетической теории или эксперимента

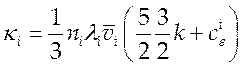                                                                            (6.20).

 - теплоемкость, соответствующая внутренним степеням свободы, множитель 5/2 перед поступательной частью теплоемкости есть поправка Эйкина, учитывающая вклад быстрых частиц.

          Длина свободного пробега определяется выражением

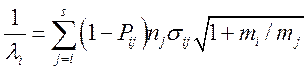                                                                   (6.21).

Параметр стойкости  учитывает тенденцию частиц сохранять после столкновения компоненту скорости в первоначальном направлении

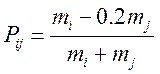                                                                                        (6.22).

          При наличии реакции ионизации в (6.19) необходимо учесть вклад электронной компоненты  в  и теплопроводность, обусловленную переносом энергии ионизации  в .

Электронная теплопроводность.

          Для слабоионизованного газа используют приближение Вальдмана:

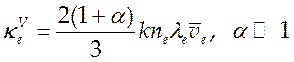                                                                               (6.23).

          Для полностью ионизованной плазмы приближение Спитцера

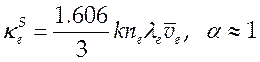                                                                                    (6.24).

В (6.23) и (6.24) 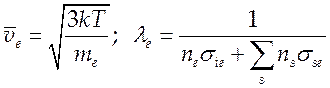;  - степень ионизации;  - сечение столкновения электрона с ионом;  - сечение столкновения электрона с нейтральной частицей сорта «s».

          В промежуточной области можно использовать сшивку:

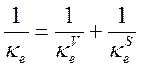                                                                                                     (6.25).

Теплопроводность, обусловленная переносом

энергии ионизации.

          Данный процесс происходит вследствие совместной диффузии электронов и ионов и называется амбиполярной диффузией. Суть ее заключается в следующем. Рассмотрим некоторый объем занимаемый полностью ионизованной плазмой. Вследствие диффузионных процессов из него будут выходить электроны и ионы, при этом, поскольку электроны легче, скорость их выхода будет выше, чем у ионов. В результате в рассматриваемом объеме возникнут не скомпенсированный электрический заряд и электрическое поле, которое будет препятствовать разделению зарядов. Это приведет к тому, что электроны и ионы начнут диффундировать совместно и для потока заряженных частиц будем иметь

                                                                                             (6.26),

где , , 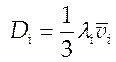 температура электронов и ионов соответственно. Величина носит название коэффициента амбиполярной диффузии. В результате амбиполярной диффузии будет переносится тепло и коэффициент теплопроводности, соответствующий этому процессу  согласно (6.17) есть

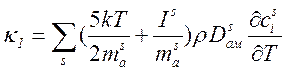                                                                      (6.27).

Здесь  энергия ионизации и масса атома сорта «s» соответственно,  массовая концентрация ионов сорта «s».

Таким образом, полный коэффициент теплопроводности для плазмы составит

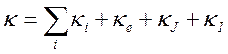                                                                    (6.28).

Статистические методы в теории переноса.

Потоковые уравнения и выражения для коэффициентов переноса можно получить, если известна функция распределения плотности вероятности. Пусть число частиц в элементе шестимерного фазового объема . Запишем полную производную по времени от функции распределения

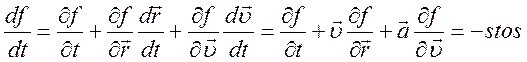                                    (6.29),

где ускорение, а внешние силы, действующие на систему; (столкновительный член) – равен разности потоков частиц приходящих и покидающих фазовый объем. В общем случае столкновительный член в явном виде выписать не удается. Это можно сделать в случае упругих парных столкновений (т. н. двухчастичное приближение).

Пусть до столкновения скорость одной частицы , другой  и соответствующие им функции распределения  и , а после столкновения  и . Обозначим через  их относительную скорость. Окружим молекулы обладающие скоростью  некой сферой действия с радиусом равным радиусу действия межмолекулярных сил. Тогда число столкновений молекулы первого сорта со всеми молекулами второго сорта в рассматриваемом объеме за единицу времени (частота столкновений) есть (см. (4.11):

                                                                             (6.30),

где сечение столкновения. Умножая (6.30) на число частиц первого сорта в элементе фазового объема -  и интегрируя по всем относительным скоростям (в данном случае по ) и прицельным параметрам получим поток частиц, приходящих в фазовый объем

, который через дифференциальное эффективное сечение  (см.(5.9)) запишется