Термодинамика и равновесный состав химически реагирующего газа

Лекция 7.

Термодинамика и равновесный состав химически реагирующего газа.

Во многих реальных процессах макроскопические параметры, характеризующие состояние газа (р, r, T, e) меняются достаточно медленно, по сравнению со скоростями релаксационных процессов, приводящих к установлению термодинамического равновесия. В таких случаях частица газа в каждый момент времени пребывает в состоянии очень близком к термодинамически равновесному, определяемому мгновенными значениями макроскопических параметров. В этом случае говорят, что газ находится в состоянии локального термодинамического равновесия (ЛТР).

Ниже будем рассматривать процессы, происходящие в химически реагирующем идеальном газе, находящемся в состоянии ЛТР.

Для того чтобы определить термодинамику газа с переменным числом частиц воспользуемся основным термодинамическим тождеством (1.25) и тем, что ,  и  есть аддитивные функции. Тогда в расчете на одну частицу имеем, 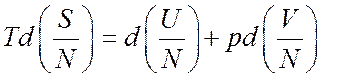откуда следует

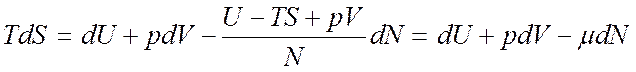                                                                                                                                                                                                     (7.1).

Величина 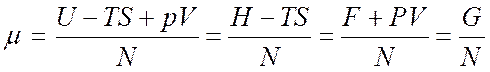 - называется химическим потенциалом. Здесь  - энтальпия;  - свободная энергия;  -  потенциала Гиббса.

        Если у нас имеется смесь газов из разных частиц, то (7.1) будет представлять:

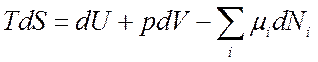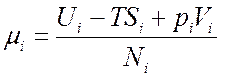                    где .                                                                                                     (7.2),

Используя (7.2) легко получить выражения для полных дифференциалов основных термодинамических потенциалов ,  и  в случае переменного числа частиц:

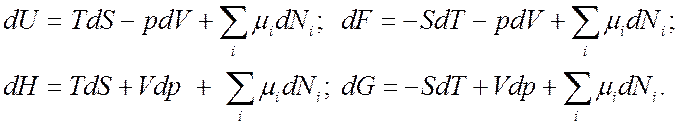                                                                                                                                                                                          (7.3).

Равновесие системы с переменным числом частиц определяется равенством нулю вариаций свободной энергии  или потенциала Гиббса  по числу частиц  , откуда согласно (7.3) следует условие

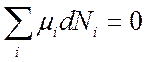                                                                                                                                                                   (7.4).

Любую химическую реакцию можно записать:

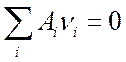                                                                                             (7.5),

где А_i – символ вещества, v_i – его доля в стехиометрической смеси (стехиометрическая смесь – это смесь, для которой реакция идет без остатка исходных реагентов), так, например,

 - так же называются стехиометрическими коэффициентами.

Для такой смеси уравнение равновесия (7.5) запишется

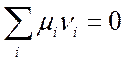                                                               (7.6).

Выражение (7.6) известно как закон действующих масс.

          Для расчета состава и всех термодинамических свойств необходимо по значениям энергетических уровней всех видов движения составить выражение для статистической суммы всей системы (большой канонический ансамбль):

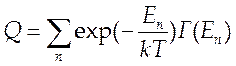                                                                                        (7.7)

          В общем случае нахождение  сводится к вычислению конфигурационных интегралов. Для идеального газа из слабовзаимодействующих частиц нескольких сортов с числом частиц  статистическая сумма распадается на произведение сомножителей

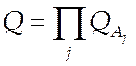                                                                                                      (7.8)

          Статистические суммы ансамблей   определяются через произведения статистических сумм отдельных частиц . Тогда для системы из одинаковых частиц

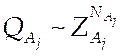                                                                                                        (7.9).

При этом все состояния, соответствующие различным перестановкам тождественных частиц, учтены, в то время как они соответствуют одной и той же энергии. Для снятия этого вырождения необходимо (7.9) разделить на число перестановок, и в итоге получаем

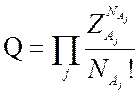                                                                                                      (7.10).

Из статической механики известно общее выражение свободной энергии для сложной системы:

                                                           (7.11).

Если в (7.10) заменить факториалы по формуле Стирлинга , то выражение для свободной энергии примет вид

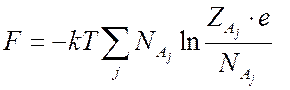                                                  (7.12).

Если учесть в идеальном  газе слабые взаимодействия, то свободную энергию такого газа можно представить в виде

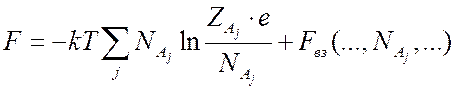                                                        (7.13).

Здесь , однако, в ряде случаев ею пренебречь нельзя, так как она может заметно сдвинуть химическое равновесие и изменить состав смеси.

Таким образом, если определена свободная энергия, т. е. известны статистические суммы частиц, то все остальные термодинамические функции можно получить из (7.3)

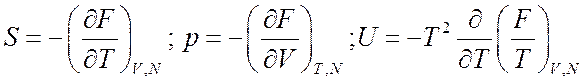                            (7.14).

Если пренебречь взаимодействием между электронными состояниями, колебанием и вращением то статистическая сумма одной молекулы распадается на произведение:

, где в квазиклассическом приближении поступательная сумма любой частицы есть:

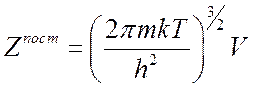                                                       (7.15),

 – масса частицы,  – объем, занимаемый газом.

Вращательная статистическая сумма для двухатомной или линейной многоатомной молекулы:

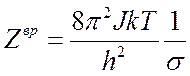                                                                (7.16),

 – момент инерции линейной молекулы,  - фактор симметрии (для двухатомной молекулы, состоящей из одинаковых атомов ).

Колебательная статистическая сумма для линейного гармонического осциллятора:

                                                           (7.17).