Стационарный пограничный слой на пластине в газовом потоке, страница 13

Сложность применения полуэмпирических подходов заключается в том, что всегда есть опасность выйти за рамки применимости метода, определенные набором эмпирической информации.

10.8. Влияние сжимаемости на устойчивость.

В связи с запросами авиационной техники, увеличением скорости и высоты полета самолетов, важным становится учет сжимаемости текущей среды на переход ламинарного течения в турбулентное. Первые попытки исследования устойчивости с учетом сжимаемости были проведены после второй мировой войны. Было получено, что при больших дозвуковых скоростях полета влияние сжимаемости незначительно. Однако для сверхзвуковых скоростей при числе Маха М > 3 пограничный слой становится все более неустойчивым. Сложности же в исследовании устойчивости сжимаемых течений росли с ростом числа Маха.

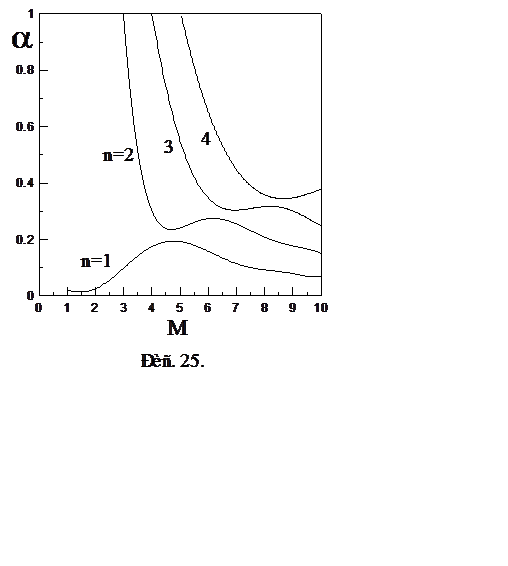В сверх- и гиперзвуковых течениях обнаруживали все новые и новые виды неустойчивости, каждая из которых могла привести к турбулизации течения. Все большую роль в неустойчивости стали играть звуковые колебания, вызывая акустические колебания пограничного слоя, которые сопровождались излучением звука от пограничного слоя. Фактически, увеличение числа Маха приводит к тому, что сохраняются основные черты неустойчивости медленных течений, но к ним добавляются все новые и новые черточки. Отметим основные из них.

Если для несжимаемых течений на линейной стадии развития неустойчивых волн быстрее всего растут двумерные волны, а трехмерные возмущения появляются на нелинейных стадиях, то в сжимаемых течениях уже в линейной области сильнее всего растут наклонные волны Толлмина-Шлихтинга. Причем угол наклона этих волн весьма велик (60⁰ – 70⁰).

Другая важная особенность неустойчивости течений для М > 3 заключается в появлении, дополнительно к известным вихревым возмущениям, неустойчивых возмущений акустической природы. Их называют маковскими модами, по имени открывшего их ученого из США Л.Мака (1969), или акустическими модами. На графике рис. 25 в координатах: волновое число - число Маха под номером n = 1 показана известная в дозвуковых течениях вихревая мода, под номерами n = 2, 3 и 4 акустические возмущения. Реально их существует гораздо больше. Эти новые возмущения являются более высокочастотными, имеют двумерный характер и ведут себя во всем прямо противоположно волнам Толлмина-Шлихтинга. То, что подавляет волны Толлмина-Шлихтинга (теплопередача и т.д.), только усиливает маковские моды и наоборот.

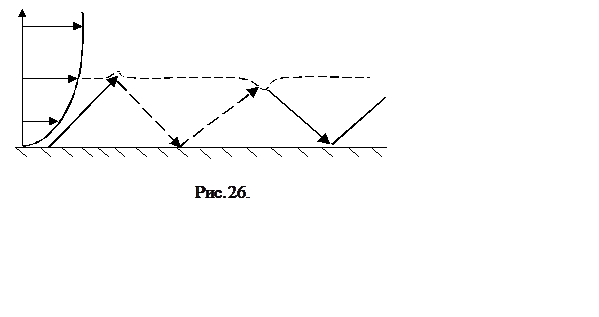Можно предложить следующую физическую интерпретацию акустической моды возмущений. В сверхзвуковом пограничном слое существует, так называемая, звуковая линия, где скорость звука и скорость потока равны (пунктир на схеме течения на рис. 26). Случайно возникшая волна давления (сплошная стрелка), падающая на звуковую линию, вызывает ее прогиб кверху и отражается от нее вниз уже как волна разрежения (пунктирная стрелка). Отражаясь от жесткой поверхности тела, она вновь падает на звуковую линию и вызывает ее прогиб вниз, отражаясь, уже как волна давления. При этом поток в прогибе над линией движется относительно потока под линией со сверхзвуковой скоростью, что и подкачивает энергию сверхзвукового движения в пограничном слое в волну давления. Далее волна давления отражается от поверхности, идет вверх и цикл распространения и усиления акустических волн повторяется. Таким образом, происходит поперечная деформация поля течения и нарастание энергии акустических волн в сверхзвуковом пограничном слое. Из-за повышения скорости потока, от нулевой у поверхности до звуковой у звуковой линии, фронты волн оказываются наклоненными к направлению течения под некоторым углом. Вследствие этого, для не слишком больших числах Маха, длина волны акустических возмущений в продольном направлении оказывается примерно равной удвоенной толщине пограничного слоя.