Стационарный пограничный слой на пластине в газовом потоке, страница 2

Сопротивление пластины для данного случая сводится к уже рассмотренному случаю плоской пластины в несжимаемом потоке

,                               (7.17)

На рис. 15 и 16 приведено несколько профилей скорости и температуры для чисел M £ 10 и теплоизолированной поверхности при показателе степени n = 0,76. При возрастании числа Маха отчетливо видно спрямление профилей скорости, рост толщины пограничного слоя и сильный нагрев поверхности.

Задача 7.1.

Вывести зависимость интегральных толщин пограничного слоя от числа Маха для теплоизолированной пластины. Считать, что число Прандтля Pr = 1, а m = Т.

Задача 7.2.

Два сверхзвуковых потока с температурами торможения T_0I, T_0II и числом Маха M_I, M_II разделены тонкой пластиной. Оценить температуру пластины. Параметры торможения заданы, число Прандтля Pr = 1 и m = Т. Дополнительное условие .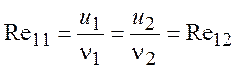

Задача 7.3.

Тонкая пластина с температурой T_w обтекается сверхзвуковым потоком с числом Маха М и температурой торможения Т₀. Найти максимальную температуру в пограничном слое.

8. ТРЕХМЕРНЫЕ ПОГРАНИЧНЫЕ СЛОИ

В данном разделе мы рассмотрим два простейших случая течений в пограничном слое, когда составляющие скорости есть во всех трех  направлениях. Расчет трехмерных течений сложен вследствие больших математических трудностей. Мы ограничимся простейшими случаями осесимметричных течений, допускающими сведение их к двумерной, уже решенной задаче. Трехмерный пограничный слой на скользящем крыле будет исследован лишь качественно.

8.1. Пространственный пограничный слой

на скользящем крыле

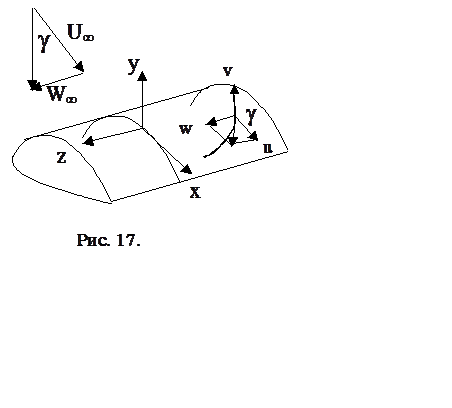Пожалуй самой простой задачей теории пространственного пограничного слоя является задача о стационарном пограничном слое на цилиндрическом теле бесконечного размаха. Выберем систему координат согласно рис. 17 и  пренебрежем ролью кривизны поверхности. В этом случае уравнения движения несжимаемого газа будут иметь вид

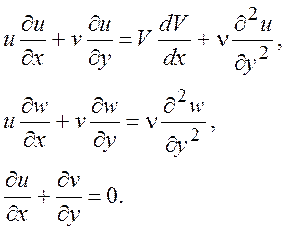                                          (8.1)

при граничных условиях

u(0) = v(0) = w(0) = 0,      u(¥) ® W(¥) = const.                        (8.2)

Система (8.1) с граничными условиями (8.2) распадается на две. Первое и третье уравнения соответствуют уже решенной плоской задаче. Второе уравнение, после определения u и v, становится линейным уравнением относительно w и служит для его определения.

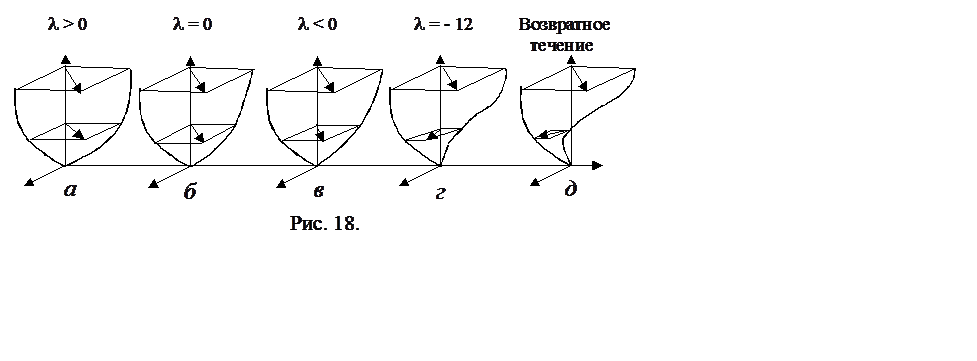Наиболее прост случай косого обтекания плоской пластины. Здесь

u(¥) = V_¥ = const,      w(¥) = W_¥ = const.                        (8.3)

Первое и второе уравнения системы (8.1) становятся тождественными по записи, из чего, с учетом граничных условий, следует:

w(x,y) = const u(x,y)                                                  (8.4)

или

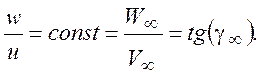                                             (8.5)

Из (8.5) следует, что направление линий тока в пограничном слое совпадает с направлением внешних линий тока. В этом случае вторичные течения отсутствуют и наклон пластины не влияет на развитие пограничного слоя.

В случае косого обтекания симметричного цилиндрического тела должны выполняться граничные условия (8.2). Не претендуя на строгость, рассмотрим сугубо качественно поведение линий тока для такого течения. Решение для первого и третьего уравнений системы (8.1) уже было найдено. Профили продольной скорости будут изменяться от сильно наполненных в области разгона потока вблизи передней кромки до отрывного профиля с нулевой производной  на поверхности. За точкой отрыва возникает возвратное течение. Соответствующие  профили нанесены на рис. 18.

Второе уравнение системы (8.1) не содержит градиент скорости внешнего течения. Можно ожидать, что профиль скорости в трансверсальном направлении будет наполненным. Предположим, что они не сильно отличаются от профиля скорости на пластине и нанесем их на рис. 18.