Сравним направление линий тока на внешней границе пограничного слоя и направление “ предельной “ линии тока на поверхности крыла. Так как на участке разгона потока (рис. 18, а) профиль скорости в продольном направлении более наполнен, чем в трансверсальном, можно ожидать, что “предельная“ линия тока отклонится от внешней и корневой части крыла. В области нулевого градиента давления (рис. 18, б) обе линии тока будут иметь одинаковое направление. В области торможения (рис. 18, в) более наполнен будет трансверсальный профиль. “ Предельная “ линия тока начнет разворачиваться по направлению к внешней части крыла. В области отрывного профиля продольной скорости течение будет направлено вдоль крыла, к его консоли (рис. 18, г). В возвратном течении (рис. 18, д) “предельная “ линия тока будет подтягиваться к линии отрыва. Положение линий тока на крыле показано на рис. 19.
Такое стекание пограничного слоя у поверхности вдоль крыла может приводить к утолщению пограничного слоя и преждевременному отрыву. Одним из способов предотвращения стекания пограничного слоя на стреловидных крыльях - установка продольных перегородок – “гребней”.
8.2. Установившиеся осесимметричные
пограничные слои
 Другой из простейших примеров трехмерного
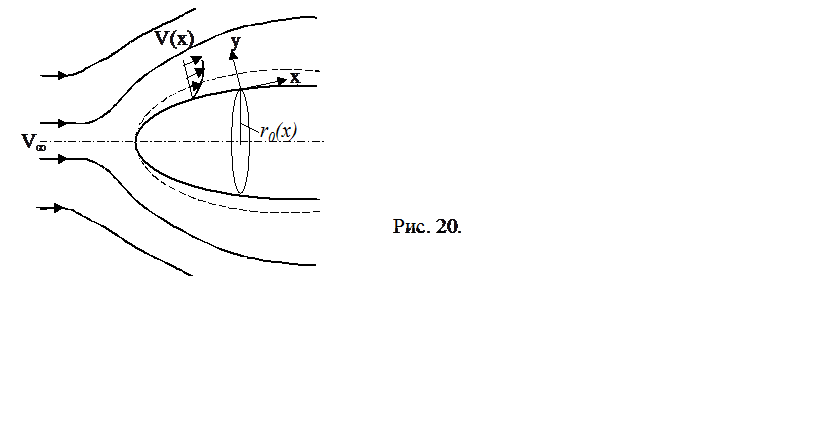
пограничного слоя – пограничный слой на теле вращения, установленном под нулевым
углом атаки (рис. 20). Такая задача легко преобразуется в соответствующую
задачу для двумерного потока. Запишем уравнения пограничного слоя в
криволинейных координатах
Другой из простейших примеров трехмерного
пограничного слоя – пограничный слой на теле вращения, установленном под нулевым
углом атаки (рис. 20). Такая задача легко преобразуется в соответствующую
задачу для двумерного потока. Запишем уравнения пограничного слоя в
криволинейных координатах
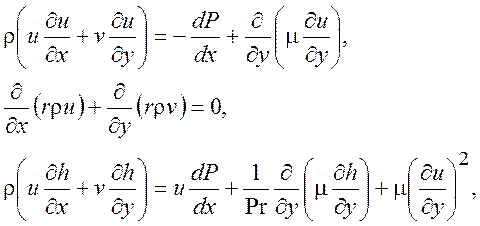 (8.6)
(8.6)
где r - радиальное расстояние.
Граничные условия остаются прежними. Потребуем, чтобы d << k-1 и d << (dk / dr)-1/2, где k - кривизна поверхности тела в меридиональном сечении. Тогда радиальное расстояние r можно заменить на радиус поверхности тела r0(x) и уравнение неразрывности в системе (8.6) примет вид:
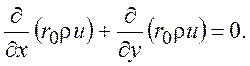 (8.7)
(8.7)
Дополнительное условие – d(x) << r0(x).
Введем функцию тока
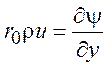 ,
, 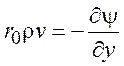 . (8.8)
. (8.8)
Преобразуем систему (8.6) к новым переменным с помощью преобразований Степанова-Манглера
![]()
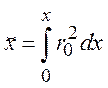 ,
, ![]() .
(8.9)
.
(8.9)
Поперечную скорость преобразуем согласно равенству
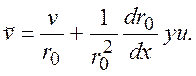 (8.10)
(8.10)
Остальные параметры потока оставим прежними
![]()
Используя выражения (8.8) и (8.10), из (8.6) и (8.7) получим
![]()
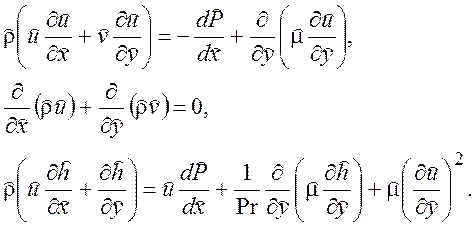 (8.11)
(8.11)
Мы получим
тот же самый вид уравнений, что и для плоского случая. В качестве решения для
данного ![]() можно использовать уже известное решение,
которое преобразованием Степанова-Манглера сводится к рассматриваемой
осесимметричной задаче.
можно использовать уже известное решение,
которое преобразованием Степанова-Манглера сводится к рассматриваемой
осесимметричной задаче.
8.3. Пограничный слой на конусе в продольном
сверхзвуковом потоке
Будем предполагать, что круговой конус обтекается сверхзвуковым потоком, параллельным оси конуса, и что при заданном числе Маха набегающего потока ударная волна присоединена к вершине конуса. За ударной волной течение газа будет потенциальным и коническим, давление на поверхности – постоянным. Так как продольный градиент давления равен нулю, задача о пограничном слое на конусе сводится к задаче о пограничном слое на пластине.
Используем преобразования Степанова-Манглера. Из равенства (8.9) получим
![]() ,
, 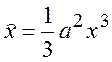 ,
, ![]() . (8.12)
. (8.12)
где ![]() (a - полуугол раствора конуса). Пограничные слои на конусе и
на пластине автомодельные. Профили продольной скорости и температуры в
автомодельных переменных задаются едиными распределениями, как для конуса, так
и для пластины. Масштабные множители, задающие связь координат конуса и
пластины определяются соотношением (8.12).
(a - полуугол раствора конуса). Пограничные слои на конусе и
на пластине автомодельные. Профили продольной скорости и температуры в
автомодельных переменных задаются едиными распределениями, как для конуса, так
и для пластины. Масштабные множители, задающие связь координат конуса и
пластины определяются соотношением (8.12).
Примем одинаковыми значения продольных координат на конусе и пластине ![]() . Это означает, что надо принять
. Это означает, что надо принять
![]() или
или ![]() (8.13)
(8.13)
Тогда нормальные к поверхности координаты связаны соотношением
![]() ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.