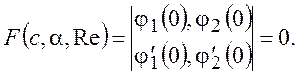Стационарный пограничный слой на пластине в газовом потоке, страница 10

                                        (10.11)

Решение (10.11) дает c = c(a, Re). Задавая различные значения Re, можно провести исследования различных течений с профилем скорости V(y), а задавая различные значения a - рассмотреть устойчивость каждого течения к возмущениям со всевозможными длинами волн. Множество точек в плоскости (a, Re), в которых c_i = 0, образует кривую нейтральной устойчивости. Наименьшее значение числа Рейнольдса на ней – Re_кр называется критическим значением числа Рейнольдса. При всех Re < Re_кр возмущения всех длин волн затухают со временем, при Re > Re_кр существует ряд волновых чисел a, при которых возмущения растут, т.е. имеет место неустойчивость.

Нейтральная кривая для течения Блазиуса приведена на рис. 22. Первоначально задача устойчивости течения Блазиуса была решена асимптотическим методом (Толлмин, 1929; Шлихтинг, 1933). В дальнейшем проводились систематические расчеты более точными численными методами. Результаты расчетов получили экспериментальное подтверждение в работе Г.Шубауэра, Г. Скрамстеда (1947). Наблюдаемые в эксперименте волны были названы волнами Толлмина-Шлихтинга.

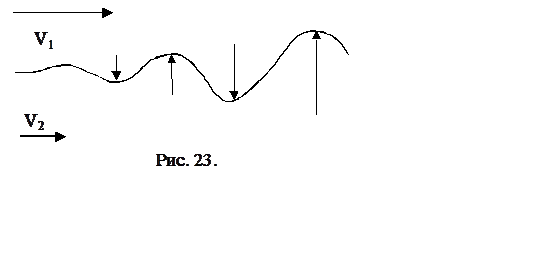Упрощенная физическая интерпретация возникновения и развития волн Толлмина-Шлихтинга приведена на рис. 23. Пусть имеется два слоя потока с разными скоростями V₁ и V₂, разделенных линией. Перейдем в систему координат, движущуюся со средней скоростью (V₁+V₂)/2. При случайном малом изгибе разделительной линии (например, вверх) площадь верхнего потока сокращается, скорость жидкости, в области изгиба, увеличивается и давление падает (согласно уравнения Бернулли). Снизу изгиба площадь потока увеличивается, скорость потока падает, давление увеличивается. Результирующие силы показаны на схеме стрелками. Оба эти процесса усиливают изгиб разделяющей линии, что приводит к дальнейшей неустойчивости такого течения. В начале силы вязкости препятствуют деформации и стабилизируют течение. При увеличении числа Рейнольдса после сечения Re = Re_кр волны растут по экспоненциальному закону до сечения, за которым начинались интенсивные нелинейные процессы, и течение переходило в турбулентное состояние.

Поведение возмущений до зоны перехода достаточно точно описывается линейной теорией устойчивости и ее можно использовать для предсказания зоны  перехода. В настоящее время развито несколько полуэмпирических методов, основанных на расчетах коэффициентов усиления возмущений (-a_i) для предсказания перехода, которые успешно применяются как при малых дозвуковых, так и при больших сверхзвуковых скоростях течения.

10.6. Нелинейная теория устойчивости

Для решения вопроса о нелинейном развитии возмущений надо решать полную нелинейную систему уравнений, полученную из уравнений движения жидкости или газа. В настоящее время достигнуты некоторые успехи в численном моделировании нелинейных процессов в простейших течениях на современных супер-ЭВМ, но задача эта очень сложна и полностью не решена до настоящего времени. Изложить в рамках одного параграфа все существующие подходы невозможно. Отметим только, что нелинейное развитие возмущений и возможные пути перехода к турбулентному режиму течения впервые были рассмотрены Л.Д.Ландау. Он предложил уравнение, описывающее изменение модуля амплитуды A возмущений во времени:

.

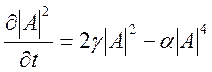Анализ этого уравнения показал, что возможно жесткое самовозбуждение системы, то есть она неустойчива по отношению к возмущениям конечной амплитуды, но устойчива к малым возмущениям. При мягком самовозбуждении, неустойчивым по отношению к бесконечно малым возмущениям, система может выйти на новый ламинарный режим, который тоже может оказаться неустойчивым. В настоящее время теория Ландау получила дальнейшее развитие при изучении бифуркаций решений, нелинейного резонансного взаимодействия возмущений и стохастизации детерминированных систем.