Стационарный пограничный слой на пластине в газовом потоке, страница 4

то есть при одинаковых х толщина пограничного слоя на пластине в  раз больше, чем на конусе и .

Сравним между собой напряжение трения s_xy для конуса и для пластины

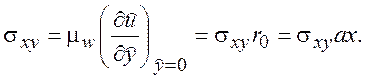                              (8.14)

Тогда из (8.14) получим, что

                                                  

Аналогичным образом вычислим

.                                           (8.15)

Толщины пограничного слоя на конусе и пластине будут совпадать, если расстояние вдоль потока на пластине взять в три раза меньше, чем на конусе. В этом случае будут совпадать распределения продольных скоростей и профили температуры.

8.4. Общий подход к проблеме пространственного пограничного слоя

          Для простоты рассмотрим пограничный слой на плоской пластине и его уравнения запишем в декартовой системе координат. Помимо координаты  вдоль обтекаемой поверхности и координаты  по нормали к ней введем еще одну координату  вдоль поверхности. В этих координатах запишем уравнения пространственного несжимаемого пограничного слоя. Коэффициент вязкости также будем полагать постоянным.

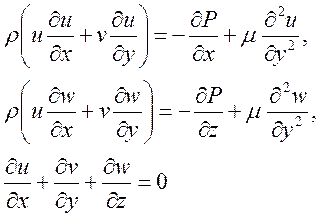                                     (8.16)

Два первых уравнения являются уравнениями движения вдоль координат на обтекаемой поверхности, а последнее уравнение есть уравнение неразрывности. Здесь давление также не зависит от координаты .

          Чтобы решить некоторую задачу с помощью этих уравнений в области  необходимо поставить граничные условия. Как и в двумерном случае на поверхности обтекаемого тела ставятся условия прилипания, т.е. задаются равными нулю все компоненты скорости. На внешней границе пограничного слоя  задается распределение давления и две компоненты скорости , параллельные поверхности тела. Чтобы выяснить, какие условия необходимо задавать на боковых границах, необходимо рассмотреть характеристические свойства уравнений.

          Пусть  характеристическая поверхность, тогда она должна удовлетворять следующему характеристическому уравнению.

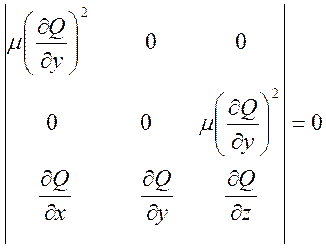                                    (8.17)

Если раскрыть определитель и приравнять его нулю, то получим одно уравнение для характеристической поверхности 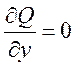. Отсюда следует, что любая поверхность , ортогональная к обтекаемой, является характеристической поверхностью и уравнение (8.16) является параболическим, как и в двумерном случае. Следовательно, как и в двумерном случае возмущения из любой точки пограничного слоя распространяются вдоль координаты  с бесконечной скоростью. Однако теория характеристик не дает информациюю, как распространяются возмущения вдоль двух других координат.

          Решение этой проблемы было предложено Вонгом в 1971 году. Он пренебрег вязкими членами в уравнении (8.16) и составил новое характеристическое уравнение. Полученные в результате характеристики он назвал субхарактеристиками. Поскольку в уравнениях движения старшими станут теперь первые производные, то характеристическое уравнение запишется в виде.

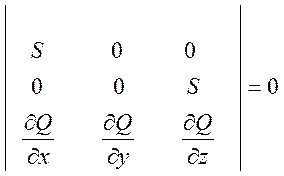                                                    (8.18)

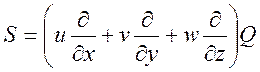где введено обозначение . Раскрывая определитель, получим уже знакомый нам корень 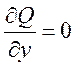 и новый . Нетрудно видеть, что последний корень соответствует линии тока в трехмерном потоке.

Рис. 20,а.

          Таким образом, нами получено, что возмущения в некоторой точке  (рис. 20,а) пространственного пограничного слоя с бесконечной скоростью распространяются вдоль нормали  к обтекаемой поверхности и далее они распространяются по потоку вдоль каждой линии тока, проходящей через эту нормаль. И с этих линий тока возмущения опять же распространяются по нормалям, проведенным через каждую их точку. Отсюда следует простое правило для зоны влияния данной точки: через нее следует провести нормаль к обтекаемой поверхности и через нее построить две поверхности, содержащие крайние линии тока, перпендикулярно обтекаемой поверхности. Область, заключенная между ними и будет зоной влияния данной точки. Аналогично строится и зона зависимости, но только против потока.