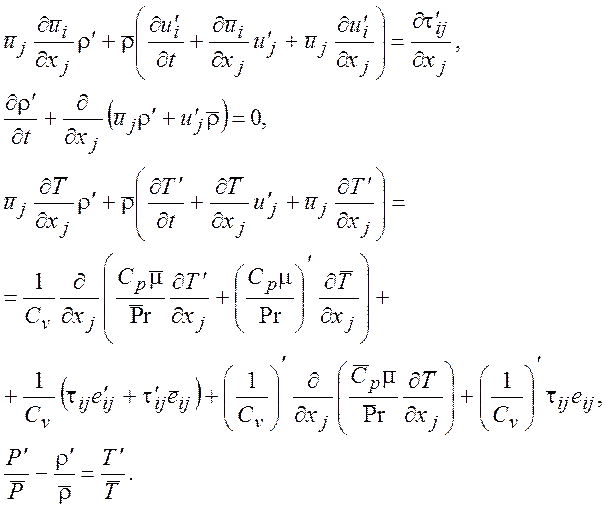 (10.2)
(10.2)
В систему (10.2) входят следующие выражения:
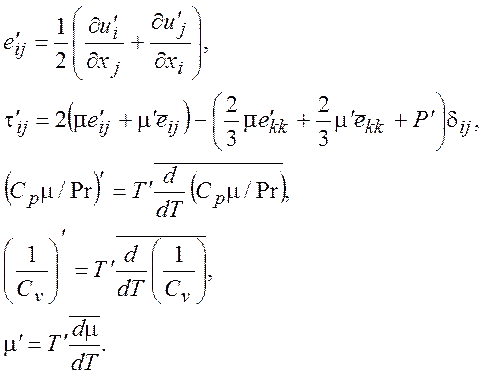
Система (10.2) описывает развитие возмущений в пространстве и времени, ее коэффициенты – известные функции, определяемые стационарным решением.
Интегрирование системы (10.2) представляет сложную задачу. Точных ее решений в настоящее время нет. Однако существует широкий класс течений, когда возможны упрощения системы. К ним относятся течения в пограничном слое, в свободных и пристенных струях, слоях смешения. Такие течения можно рассматривать как близкие к параллельным.
10.3. Приближение параллельного течения
Пусть течение осуществляется в направлении x1, а параметры потока зависят только от x2. Тогда частные решения системы (10.2) можно записать в виде
![]() , (10.3)
, (10.3)
здесь a и b - волновые числа возмущения, c - фазовая скорость. В общем случае a, b и ac - комплексные числа. Если рассматривать решения для действительных a, b и комплексных c, то мы будем изучать возмущения, растущие во времени (временная неустойчивость). В большинстве реальных течений возмущения растут не во времени, а в пространстве (пространственная неустойчивость). Такие течения описываются при реальных ac и комплексном a. В первом случае устойчивость течения определяется знаком Im c = ci, во втором – знаком Im a = ai.
Подстановка выражения (10.3) в систему (10.2) приводит к системе обыкновенных дифференциальных уравнений, которая очень громоздка. Однако, если учесть, что неустойчивость возникает при больших числах Рейнольдса и пренебречь членами, содержащими множитель 1/Re в безразмерной записи уравнений (кроме члена со старшей производной), мы получим следующую систему уравнений:
![]()
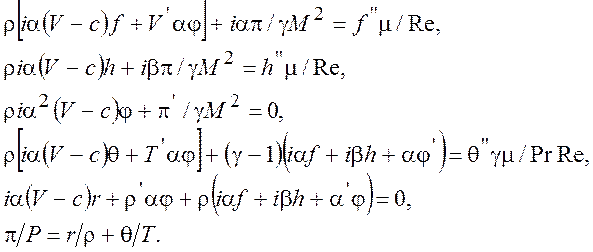 (10.4)
(10.4)
Здесь V, r, T, m, P - осредненные скорость, плотность, температура, вязкость, давление; f, aj, h - амплитуды возмущений скорости (продольной, нормальной, боковой (трансверсальной)); p, q, r - амплитуды возмущений давления, температуры, плотности; М – число Маха, Re, Pr - число Рейнольдса, построенное по толщине пограничного слоя, и Прандтля; штрих означает дифференцирование по координате y = x2/d.
Граничные условия задачи (10.4) зависят от конкретного течения. Для течения в пограничном слое их можно взять в виде
f(0) = j(0) = q(0) = 0. (10.5)
f, j, q ограничены при y ® ¥.
10.4. Уравнение Орра-Зоммерфельда
Рассмотрим более простой случай развития двумерных возмущений в несжимаемой жидкости. В системе (10.4) останутся существенными следующие уравнения:
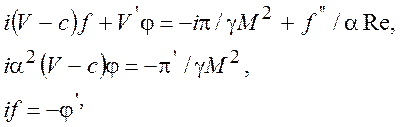 (10.6)
(10.6)
которые можно свести в одно дифференциальное уравнение
![]() (10.7)
(10.7)
Уравнение (10.7) представляет собой упрощенный аналог известного уравнения Орра-Зоммерфельда
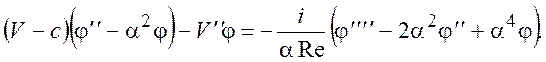 , (10.8)
, (10.8)
из которого исключены члены с множителем 1/Re при производных низших порядков.
10.5. Задача на собственные значения
Решение (10.4) с граничными условиями (10.5) представляет собой классическую задачу на собственные значения, в которой с является искомым собственным значением для каждой пары величин (a, Re).
Рассмотрим, например, устойчивость течения несжимаемой жидкости в пограничном слое на пластине. Для определенности предположим, что возмущения развиваются во времени (a- вещественное, c - комплексное). Граничные условия (10.5) можно принять в виде
j(0) = j’(0) = j(¥) = 0. (10.9)
Так какV(¥) = V¥ = const, уравнение (10.8) вдали от поверхности переходит в уравнение с постоянными коэффициентами. Его решение вне пограничного слоя, удовлетворяющее третьему условию (10.9), будет
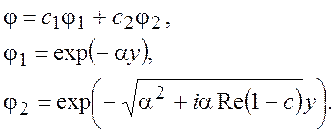 (10.10)
(10.10)
После того как численным или аналитическим методом найдены решения j1 и j2 в области пограничного слоя, необходимо подобрать такие константы c1 и c2, чтобы выполнялись два оставшихся условия (10.9) на поверхности. Эти условия дают уравнение для определения c
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.