Стационарный пограничный слой на пластине в газовом потоке, страница 5

          Из данного представления о построении зоны влияния следует простое правило задания граничных условий на боковых границах рассматриваемой области. На каждой из них следует задавать все три компоненты скорости, если газ втекает через нее в рассматриваемую область, в противном случае граница свободна от граничных условий. Как и в двумерном случае на обтекаемой поверхности необходимо задать все компоненты скорости, а на внешней границе – все компоненты, кроме нормальной к ней.

          В случае сжимаемого газа к системе уравнений (8.16) добавляется уравнение энергии, содержащее температуру. Эта система имеет те же характеристические свойства. Поэтому правило задания граничных условий на боковых границах для нее сохраняется с той лишь разницей, что к заданию компонент скорости добавится температура. Ее задание добавится также на стенке и внешней границе.

8.5. Аналогия между теплопередачей и сопротивлением тела

Все решения уравнений двумерного ламинарного пограничного слоя в несжимаемой жидкости для распределения скорости будут иметь вид

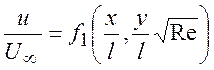                                                                                     (8.19)

Аналогично все решения для профиля температуры будут иметь вид

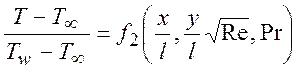                                 .                                       (8.20)

Поэтому для плотности потока тепла к поверхности, используя (8.20), получим

                                 .

Тогда для локального числа Нуссельта получим выражение

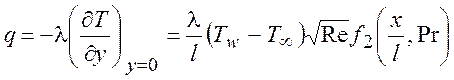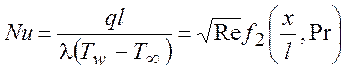                                                                   (8.21)

С использованием выражения (8.19), для локального касательного напряжения получаем

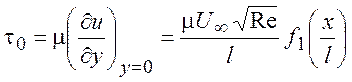                       .                                                    (8.22)

Отсюда безразмерный локальный коэффициент сопротивления будет равен

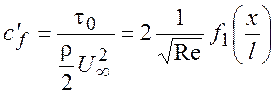                                                                          (8.23)

Скомбинировав (8.21) и (8.23), в предположении одинаковой функциональной зависимости f для скорости и температуры, получим

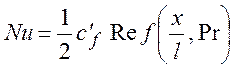                                 .                                                (8.24)

Это есть, так называемая, аналогия Рейнольдса в общей форме. Для течения на пластине при числе Прандтля равном единице профиль скорости и температуры совпадают. Тогда

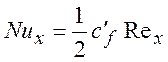                                                                                            (8.25)

Следует отметить, что аналогия Рейнольдса действует и в турбулентном течении.

Задача 8.1.

Найти какому плоскому течению соответствует течение в окрестности критической точки, где r(x) = x; U(x) = u₁x.

9.  СПУТНОЕ ТЕЧЕНИЕ ЗА ПЛАСТИНОЙ

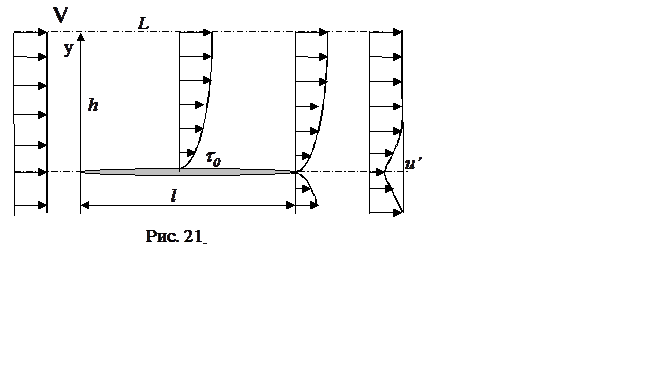Рассмотрим течение в следе на большом удалении от тела. Для простоты примем за тело плоскую пластинку длиной l. Обозначим через V скорость однородного потока (рис. 21).

Пример такого течения интересен тем, что уравнения пограничного слоя остаются справедливыми в отсутствие стенок, так как изменение характеристик течения вдоль по потоку происходит намного медленнее, чем поперек. Наличие стенки – не обязательное условие применимости уравнений пограничного слоя. Надо только, чтобы характерные поперечные размеры течения были намного меньше продольных размеров. Будем считать скорость небольшой, так что жидкость можно рассматривать несжимаемой, давление постоянным (P(x) = const). Тогда движение описывается  системой уравнений

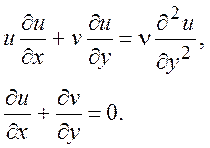                                          (9.1)

Граничные условия

u(¥) = V,   v(0) = 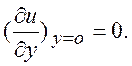                        (9.2)

Последнее условие следует из симметрии течения.

Система (9.1) с граничными условиями (9.2) имеет очевидное решение u = V, которое означает, что на очень большом удалении от тела течение полностью выравнялось. Это решение нас не интересует.

Будем искать нетривиальное решение вдали от тела, для которого выполняется некоторый “закон сохранения”. Обратимся к выводу интегрального условия импульсов (6.4). Интегрирование выражения (6.3) будем проводить в пределах от -¥ до ¥. Тогда, с учетом того, что V = const, а , получим