Лекция №5
Столкновение частиц. Сечение рассеяния. Эффективное сечение столкновений.
Определение сечений столкновения естественным образом связано с рассмотрением самого процесса столкновений частиц. Для не слишком плотного газа (р≤100 атм) вероятность трехчастичных столкновений много меньше двухчастичных и ниже мы будем рассматривать только парные столкновения.
В основе
процессов столкновений лежит взаимодействие молекул друг с другом. Хорошо
известно, что две молекулы притягиваются друг к другу, когда они удалены друг
от друга и отталкиваются при сближении на достаточно близкое расстояние. Силы
взаимодействия между молекулами являются функцией межмолекулярного расстояния r. В большинстве случаев удобнее пользоваться
потенциальной энергией взаимодействия ![]() , нежели
силой взаимодействия
, нежели
силой взаимодействия ![]() . Эти функции связаны между собой
простым соотношением
. Эти функции связаны между собой
простым соотношением 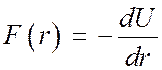 . Рассмотрим пространственное
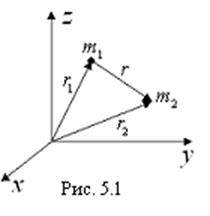
движение двух взаимодействующих частиц (рис.5.1) с массами
. Рассмотрим пространственное
движение двух взаимодействующих частиц (рис.5.1) с массами ![]() и
и ![]() соответственно,
которое подчинено уравнениям Ньютона
соответственно,
которое подчинено уравнениям Ньютона
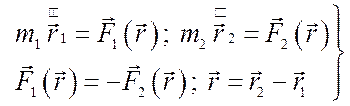 (5.1).
(5.1).
Умножим первое уравнение на m2, второе на m1 и вычтем первое из второго. В результате получим:
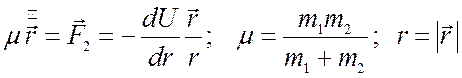 (5.2),
(5.2),
то есть задача о движении двух частиц
свелась к задаче о движении одной частицы, с приведенной массой m в центральном поле с потенциалом ![]() .
.
При движении
частицы с массой m
в центральном поле сохраняется момент количества движения ![]() относительно центра поля,
относительно центра поля, 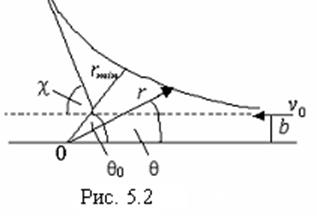 следовательно, движение частицы
происходит в одной плоскости. Введем в этой плоскости полярную систему
координат (рис. 5.2): Уравнение сохранения момента количества движения и энергии
примут вид
следовательно, движение частицы
происходит в одной плоскости. Введем в этой плоскости полярную систему
координат (рис. 5.2): Уравнение сохранения момента количества движения и энергии
примут вид
![]() (5.3),
(5.3),
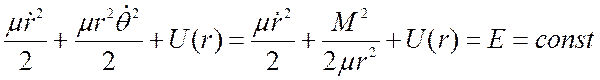 (5.4),
(5.4),
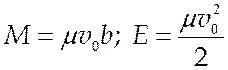 (5.5),
(5.5),
где v0 – скорость налетающей частицы, b – прицельный параметр. Исключая из (5.3) время с помощью (5.4) и интегрируя, получим:
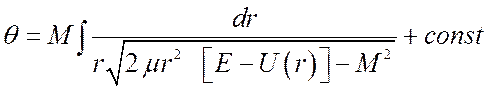 (5.6).
(5.6).
Обычно интересуются углом отклонения
![]() (5.7),
(5.7),
где 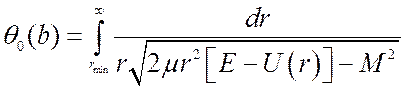 ; rmin–
соответствует минимуму потенциальной энергии.
; rmin–
соответствует минимуму потенциальной энергии.
Для
молекул со степенным законом взаимодействия U = ![]() получим:
получим:
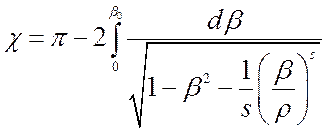 ,
,
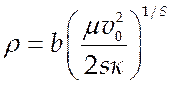 (5.8),
(5.8),
где: 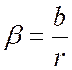 и
и 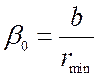 определяется
из уравнения
определяется
из уравнения 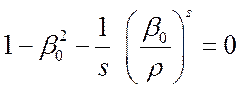 .
.
Уравнение (5.7)
(и соответственно (5.8)) задает связь угла отклонения c от прицельного параметра b и скорости налетающей частицы v0. Часто процесс рассеяния
характеризуют эффективным сечением рассеяния. Рассмотрим молекулы, пролетающие
через кольцо, лежащие между кругами b и b + db в плоскости
перпендикулярной относительной скорости v0. Все эти молекулы рассеиваются в
интервал углов между c
и c + dc, или в телесный угол ![]() . Предположим, что c и b однозначно связаны соотношениями (5.7) или (5.8).
Дифференциальным эффективным сечением
. Предположим, что c и b однозначно связаны соотношениями (5.7) или (5.8).
Дифференциальным эффективным сечением ![]() называют
площадь кольца, приходящегося на единицу телесного угла W то есть
называют
площадь кольца, приходящегося на единицу телесного угла W то есть 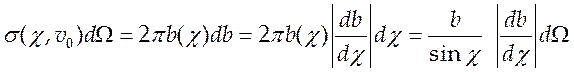 , и
, и 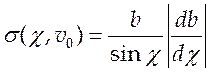 .
.
Полное эффективное сечение равно:
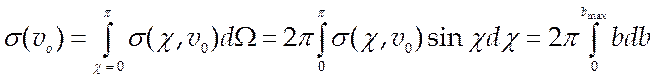 (5.9),
(5.9),
где bmax – такое прицельное расстояние, что при b ≥ bmax потенциал U = 0. Молекулы, у которых bmax конечно, называются молекулами с конечным радиусом действия. Этому условию удовлетворяют только твердые шары.
В то же время
в результате столкновений часто остается конечным изменение импульса, энергии и
других величин. Например, изменение продольного импульса молекулы в системе
центра инерции равно ![]() . В качестве осредненной
характеристики изменения импульса вводят эффективное сечение:
. В качестве осредненной
характеристики изменения импульса вводят эффективное сечение:
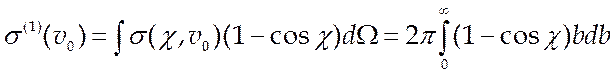 (5.10),
(5.10),
часто называемое транспортным
сечением. Для твердых сфер s(1)=pd2. Для молекул со степенным законом взаимодействия из (5.8)
и (5.10) следует: 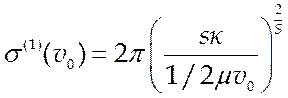 А1(s), где А1(s) определяются путем численного
А1(s), где А1(s) определяются путем численного
|
S |
А1(s) |
|
4 |
0.298 |
|
6 |
0.306 |
|
12 |
0.321 |
интегрирования и приведены в таблице. Важно отметить, что молекулу нельзя охарактеризовать каким-либо одним эффективным сечением, так как для различных видов взаимодействия (по отношению к изменению импульса, энергии и т.д.) они различны, однако поскольку все они имеют один порядок, то при качественных рассмотрениях часто можно говорить просто об эффективном сечении данной молекулы.
Потенциалы взаимодействия.
Определение потенциалов для сил, с учетом сложной структуры молекул, межъядерных взаимодействий с учетом электронных оболочек, представляет значительные трудности, и на практике обычно пользуются модельными, эмпирическими и полуэмпирическими законами взаимодействия. При выборе межмолекулярного потенциала для расчета различных величин необходимо иметь в виду два фактора: степень требуемого приближения к действительности и вычислительные трудности, связанные с использованием той или иной функции.
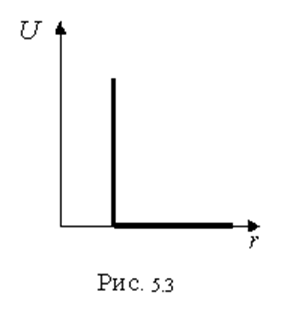 1.
Твердые непроницаемые сферы (упругие шары)
1.
Твердые непроницаемые сферы (упругие шары)
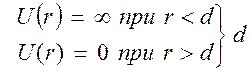 - диаметр сферы.
- диаметр сферы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.