Столкновение частиц. Сечение рассеяния. Эффективное сечение столкновений, страница 2

Эта модель дает лишь грубое представление о сильных короткодействующих силах отталкивания (т.е. о том, что молекулы обладают  объемом), тем не менее, она часто употребляется в расчетах благодаря своей простоте, особенно при рассмотрении процессов столкновений, (так как для твердых шаров процесс столкновений представляется наиболее наглядно). Более того, при применении других, более сложных законов взаимодействия обычно вводят т.н. эффективные сечения столкновений, с помощью которых столкновение реальных молекул заменяется столкновением, в некотором смысле, эквивалентных им упругих сфер. В качественных рассуждениях иногда молекулы можно рассматривать как упругие сферы с фиксированным диаметром. Это во многих случаях допустимо, т.к. диаметры эквивалентных сфер (эффективных сечений) для различных типов взаимодействия имеют одинаковый порядок (диаметры молекул имеют порядок 10^-8 см).

2. Точечный центр отталкивания

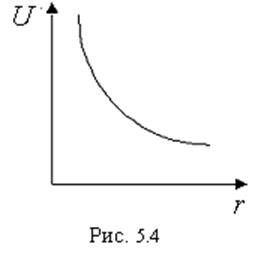
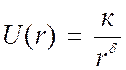: величина d называется показателем отталкивания.

Благодаря чисто математическим удобствам широкое распространение получили гипотетические молекулы с показателем , называемые  максвелловскими. Газ, состоящий из таких молекул, называют максвелловским газом. Ближе к реальным значения d лежат между 9 и 15. Максвелловские молекулы слишком «мягкие», в то время как упругие сферы слишком «твердые». Реальные потенциалы взаимодействия лежат между этими двумя наиболее распространенными модельными потенциалами.

3. Прямоугольная потенциальная яма

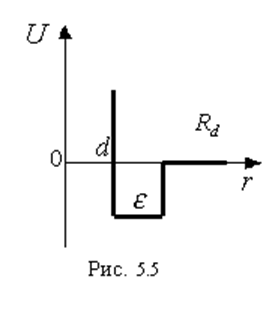
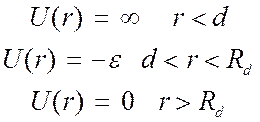
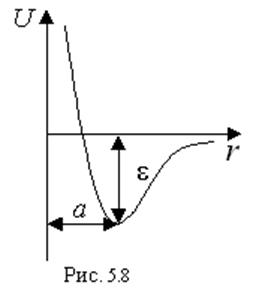
 Эта модель представляет собой твердую сферу диаметром d, окруженную слоем с полем притяжения величиной , этот слой простирается до расстояния R_d. Таким образом, в несколько грубом виде принимается в расчет, как сила отталкивания, так и сила притяжения. Эта модель дает иногда хорошее согласие для сложных молекул, так как в нее входят три произвольных (подгоночных) параметра.

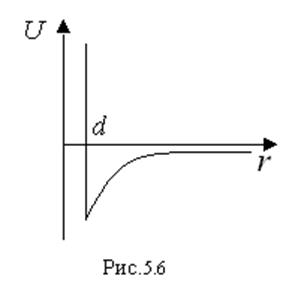4. Модель Сюзерленда

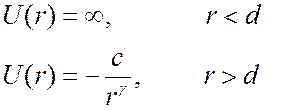
Этот потенциал описывает твердые сферы диаметром d, которые притягиваются друг к другу по закону обратной пропорциональности некоторому значению степени расстояния. Это довольно реальная модель, достаточно простая в обращении.

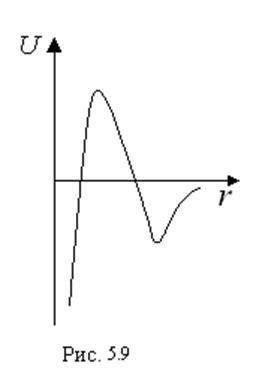
5. Потенциал Леннарда-Джонса

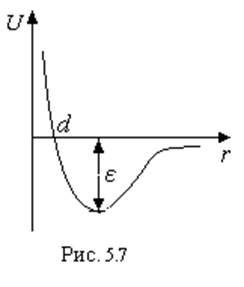
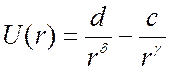; первое слагаемое описывает энергию отталкивания, второе – энергию притяжения. d и с – константы. Чаще всего используется так называемый (6 – 12) потенциал Леннарда-Джонса 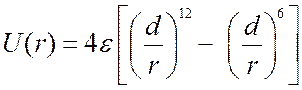; при . Величине e - максимальное значение энергии притяжения (или глубина потенциальной ямы), которое достигается при r = 2^1/6 d. Шестая степень убывания потенциала моделирует электростатическое диполь-дипольное взаимодействие. Двенадцатая степень убывания отталкивающего потенциала выбрана из соображения математического удобства и в то же время она моделирует достаточно жесткое отталкивание.

6. Потенциал Морзе

, здесь величина а определяет положение минимума потенциальной ямы, e - глубина потенциальной ямы. b - определяет кривизну потенциальной кривой вблизи минимума. С помощью этих параметров потенциальная кривая может быть удовлетворительно аппроксимирована вблизи минимума, однако этот потенциал неправдоподобно быстро спадает при r > ¥. Этот потенциал удобен во многих случаях для расчетов.

7. Потенциал Букингема

. Эта функция с четырьмя параметрами учитывает диполь-дипольное взаимодействие (второй член), диполь-квадрупольное взаимодействие (третий член), а для составляющей потенциала, связанной с отталкиванием, дает приближение в виде экспоненциального члена. Эта модель ближе к действительности, нежели модель Леннарда-Джонса, но более сложна при численных расчетах. Этот потенциал дает нереальные значения вблизи нуля, где он стремится к бесконечности.

Применяются также и другие, более сложные потенциалы с большим числом свободных параметров, которые определяются экспериментально.

Оценка эффективных сечений столкновений.

Рассмотрим два примера, иллюстрирующих подходы к оценке сечений.

1. Молекулы реального газа взаимодействуют по закону U = 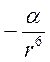 (модель Сюзерленда, силы притяжения Ван-дер-Ваальса). Обратимся непосредственно к уравнениям (5.3) - (5.5), которые в нашем случае есть:

                                                                            (5.11),

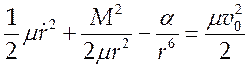                                                                  (5.12).

Тогда если под столкновением понимать соударение двух молекул, то есть в момент столкновения положить и r = d, где d – диаметр молекулы то из (5.11) будем иметь:

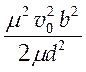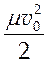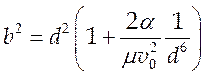 -  = , откуда  и

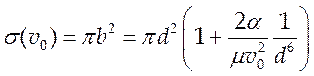                                                        (5.13).

Для того, чтобы получить эффективное сечение нужно (5.13) усреднить по всем скоростям  налетающих частиц.

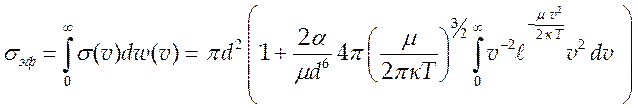
и окончательно для s_эф. имеем:

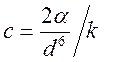,                                                        (5.14).

Поправку  называют поправкой Сюзерленда.

2. Оценим по порядку величин эффективное сечение соударений электронов с ионами в плазме. Оценку проведем, пренебрегая эффектами дальнего взаимодействия, то есть отклонениями электрона на малые углы и будем рассматривать лишь те взаимодействия, для которых кинетическая энергия налетающих электронов сравнима с потенциальной энергией взаимодействия (отклонения на большие углы), то есть 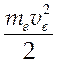   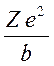 ~ . Откуда   b ~  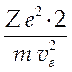и

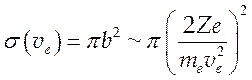                                                                 (5.15).

Здесь Z – зарядовое число, е – заряд электрона, m_e – масса электрона и m = т_е вследствие того, что масса иона много больше массы электрона. Для того, чтобы получить s_эф. необходимо усреднить (5.15) по всем скоростям в диапазоне . Для оценки мы воспользуемся значением 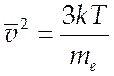 и получим

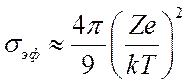                                                                          (5.16).