Приведенная ниже математическая модель построена при следующем допущении: рассмотрена стационарная ситуация с учетом различного содержания влаги в паре по сечению проточной части турбины. Данное допущение существенно упрощает математическую модель.
С использованием предлагаемой модели был проведен анализ распределения ионогенных примесей (типа натрия), кремниевой кислоты (SiO2) и продуктов коррозии (в пересчете на Fe3O4) по тракту барабанных котлов.
В установившемся режиме работы скорость прохождения веществом водного объема котла, включая реакции, протекающие в объеме, осаждение, смыв отложений и т.д., должна быть равна скорости его поступления в объем – в противном случае стационарный режим поведения вещества не будет обеспечен. Концентрация примеси на входе в котел регламентируются соответствующими нормами ее содержания в питательной воде, конкретными условиями эксплуатации, и по этой причине, не является рассчитываемым параметром в данной модели. Расчету подлежит концентрация примеси в водном объеме котла, а имея в виду контур в целом, в регенерационных отборах пара из турбины, поступающего в подогреватели высокого и низкого давления, а также в конденсате турбины.
Упрощенная тепловая схема энергоблока с барабанным котлом, на основе которой была построена математическая модель, приведена на рисунке 4.2.
Для данной модели сделаны некоторые дополнительные допущения. Концентрация примеси одинакова во всем объеме котла. Для расчета концентрации примеси в объеме котла составлены уравнения материального баланса с учетом всех путей поступления и выхода примеси из водного объема котла. Концентрация примеси в котловой воде обусловлена ее содержанием в питательной воде. Вывод примеси из котла осуществляется непрерывной продувкой. Также учитывается механический унос примеси с каплями воды в пар и распределение примеси между жидкой и паровой фазами. Концентрация примеси в конденсате рассчитывается с учетом возможных присосов в конденсаторе. Кроме того, в математической модели учитываются процессы образования отложений.
Ниже приведены уравнения материального баланса по участкам тракта энергоблока с барабанным котлом.
Уравнение материального баланса для котла в соответствии с упрощенной тепловой схемой, представленной на рис.4.2, будет иметь следующий вид:
SПВ aПВ - SКА aПРОД - SКА aКА (КР,КА + w) - SКА aКА РКА = 0 (4.27)
где:
SПВ – концентрация примеси в питательной воде, мкг/дм3;
aПВ – расход питательной воды, кг/с;
SКА – концентрация примеси в котловой воде, мкг/дм3;
aПРОД – расход непрерывной продувки, кг/с;
aКА – паропроизводительность, кг/с;
КР,КА – коэффициент распределения примеси между жидкой и паровой фазами котловой воды на линии насыщения;
w - влажность генерируемого котлом пара;
РКА – коэффициент образования отложений на поверхностях нагрева котла.
В данной математической модели коэффициент образования отложений обратно пропорционален растворимости исследуемой примеси в теплоносителе.
В общем виде, согласно [31] растворимость примеси в воде и паре может быть представлена как функция термодинамических характеристик растворителя следующим образом:
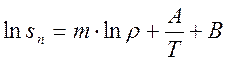(4.28)
где:
sП - растворимость исследуемой примеси в Н2О, мкг/дм3;
m - координационное число, т.е. среднестатистическое число постоянно сменяющихся молекул Н2О, составляющих в паровом растворе непосредственное окружение молекул и ионов;
А и В - некоторые коэффициенты, характерные для определенной примеси
r - плотность теплоносителя, г/см3;
Т - температура теплоносителя, К.
Таким образом, уравнение для коэффициента образования отложений будет иметь следующий вид:
P=g 1/sп (4.29)
где:
g - эмпирически определяемый коэффициент, характерный для каждого определенного тракта котла.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.