Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных")

9. методы регрессионного анализа

9.1. Сущность и задачи регрессионного анализа

Регрессионный анализ – совокупность статистических методов обработки экспериментальных данных, позволяющих в условии стохастической зависимости исследуемой величины от неслучайных или случайных переменных определять данную зависимость.

В дальнейшем будем рассматривать две модели регрессионного анализа (РА).

Модель 1. В данной модели зависимая переменная  – случайная величина, а независимые переменные x_j,  – неслучайные, точно заданные переменные. Таким образом, модель 1 регрессионного анализа имеет вид  (8.1.2).

Модель 2. В данной модели как зависимая переменная, так и независимые переменные являются случайными величинами. Следовательно, модель 2 регрессионного анализа имеет вид (8.1.4).

В дальнейшем регрессионный анализ на основе модели 1 будем называть РА-1, а на основе модели 2 – РА-2. В некоторых источниках РА-2 принято объединять с корреляционным анализом. В данной брошюре РА-2 рассматривается как самостоятельный вид регрессионного анализа, при выполнении которого привлекаются методы корреляционного анализа. Так как РА-1 и РА-2 имеют много общего, то основное внимание уделяется методам РА-1, а для РА-2 показывается лишь специфика соответствующих методов анализа.

Сущность регрессионного анализа состоит в замене стохастической зависимости между переменными  и ,  некоторой детерминированной зависимостью f, достаточно хорошо аппроксимирующей основные свойства исходной стохастической зависимости. В дальнейшем переменные ,  будем обозначать также вектором . Иначе говоря, в процессе регрессионного анализа устанавливается аналитическая зависимость между некоторой характеристикой случайной величины  и независимыми переменными . Очевидно, что в данном случае возникает проблема выбора соответствующей характеристики случайной величины . В регрессионном анализе в качестве такой характеристики используется условное математическое ожидание

случайной величины  при условии, что независимые переменные  приняли определённые значения X_<k>. Таким образом, сущность регрессионного анализа состоит в замене зависимостей вида (8.1.2) или (8.1.4) зависимостью вида

                                 .    (9.1.1)

Выражение (9.1.1) называется регрессией, именно это название и определило наименование методов, объединённых в регрессионном анализе.

Замена стохастической зависимости регрессионной определяет и ограниченность методов регрессионного анализа. Она состоит в том, что данные методы позволяют провести не всестороннее исследование того, как зависит  от , а лишь один аспект этой стохастической зависимости. Всесторонний анализ имел место, если бы, например, устанавливалась зависимость между законом распределения случайной величины  и переменными . Тем не менее, с практической точки зрения этот единственный аспект в большинстве случаев является наиболее существенным.

Можно провести классификацию видов регрессионного анализа.

По виду функции f в выражении (9.1.1) регрессионный анализ принято делить на линейный, в котором указанная функция является линейной относительно оцениваемых параметров, т.е.

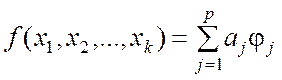                                          ,             (9.1.2)

и нелинейный, в котором она нелинейная относительно параметров a_j. В выражении (9.1.2) функции j_j могут определяться одной, несколькими или всеми независимыми переменными.

По числу независимых переменных регрессионный анализ принято подразделять на однофакторный, если имеет место только одна такая переменная, и многофакторный, если число независимых переменных более одной.

Очевидно, что для установления зависимости (9.1.1) необходимо решить ряд задач, которые и составляют собственно регрессионный анализ. К их числу относятся:

1) выбор класса функций, в рамках которого определяется взаимосвязь между  и ;

2) определение подходящих значений параметров a_j, определяющих конкретный вид функции;

3) оценка точности аппроксимации зависимости (8.1.2) или (8.1.4) функцией (9.1.1).

Необходимо отметить, что первая из перечисленных задач формально не решается методами регрессионного анализа. Иначе говоря, класс функции Y определяется на основе соображений, которые находятся вне рамок данных методов. Регрессионный анализ позволяет только оценить, насколько удачен этот выбор. При этом наилучшей оценкой зависимости  от X_<k> в заданном классе Y является функция, реализующая минимум математического ожидания квадрата ошибки, т.е. величины

                                      .         (9.1.3)

Оценка  случайной величины , принадлежащая определённому классу функций Y и минимизирующая ошибку (9.1.3), называется средней квадратической регрессией  на X_<k> класса Y.

Вместе с тем некоторые рекомендации по выбору класса функций Y могут  быть сделаны на основе анализа совокупности результатов наблюдений, в частности, при построении выборочной кривой регрессии. Это можно сделать, по крайней мере, на качественном уровне.

9.2. Однофакторный регрессионный анализ