Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 14

Пересчёт выполняем в том же порядке, который приведён выше (сохраняем ту же нумерацию пунктов).

1. Функция регрессии в данном случае представляет собой линейный алгебраический полином от одной независимой переменной

                                                    y = b₀ + b₂x₂.                     (9.3.31)

2. Составляем табл.9.12 экспериментальных данных с центрированными значениями фактора x₂.

Таблица 9.12

Массив экспериментальных данных с центрированными значениями фактора

	–4	–2	1	–0,5	0,5	5
y	–15,1	–1	19,9	9,5	16,5	47,9

Коэффициенты регрессии предварительно оцениваем в уравнении

                                                    .                    (9.3.32)

3. Система нормальных уравнений принимает вид

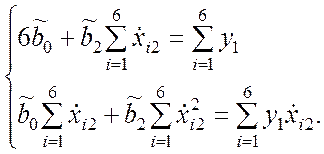                                                (9.3.33)

4. Матричное уравнение, эквивалентное системе (9.3.33), представляется как

                                       ,        (9.3.34)

где

;

;

.

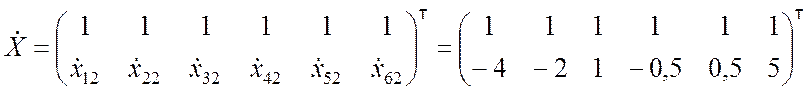Оценки коэффициентов регрессии определяются равенством

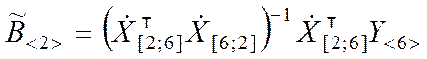                                . (9.3.35)

Вычисляем матрицу :

       

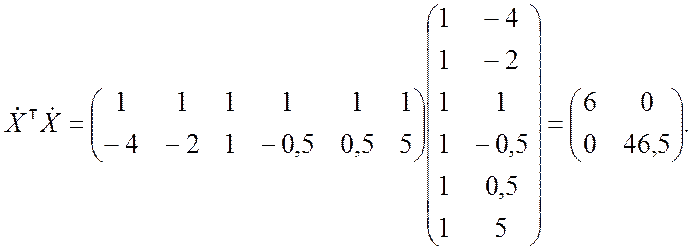
Находим обратную матрицу:

                                         .                     

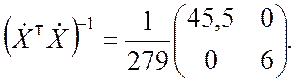Матрица в правой части уравнения (9.3.33) есть не что иное, как вектор-столбец с двумя компонентами:

                  

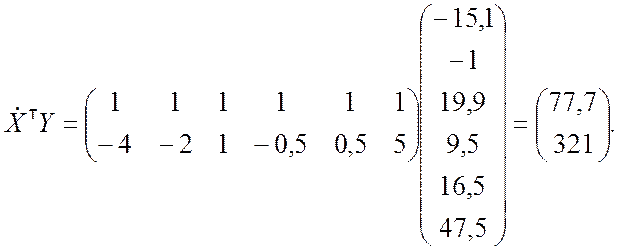
Оценку вектора коэффициентов регрессии находим по формуле (9.3.35):

                                  .

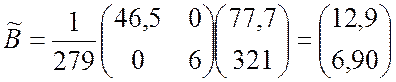Получим уравнение регрессии с одним фактором

                                                 .                  (9.3.36)

5. Проверяем адекватность уравнения (9.3.36) экспериментальным данным.

Для вычисления оценки дисперсии (9.3.19) составляем расчётную табл.9.13. Оценка дисперсии (9.3.18) остаётся прежней.

Таблица 9.13

Расчётная таблица

	yi
–4	–15,1	–14,7	–0,4	0,16
–2	–1	–0,9	–0,1	0,01
1	19,9	19,8	0,1	0,01
–0,5	9,5	9,4	0,1	0,01
0,5	16,5	16,3	0,2	0,04
5	47,9	47,4	0,5	0,25

Получаем оценку остаточной дисперсии:

                                     .

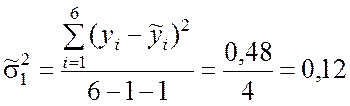Показатель согласованности (9.3.17) принимает значение

                                             .

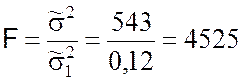Критическое   значение   данного   показателя   при   a = 0,01,   f₁ = n – 1 = 5,   f₂ = n – k – 1 = 4  составляет  F_(0,01;5;4) = 15,52.  Поскольку имеет место неравенство F > F_(0,01;5;4), нулевая гипотеза об адекватности функции регрессии (9.3.31) экспериментальным данным принимается.

6. Выполняем селекцию факторов. Главная диагональ корреляционной матрицы (9.3.22) с учётом выражений (9.3.28) и (9.3.30) принимает вид

                                .

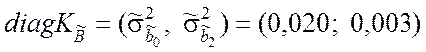Из полученного результата следует, что

                                          .

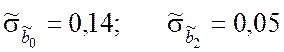Наблюдаемые значения показателя согласованности (9.3.21) для факторов   и :

                        .

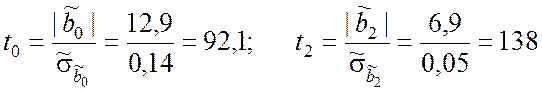Находим критическое значение данного показателя в приложении 6, оно составляет t_(0,01;4) = 4,6. Таким образом,

                                           t₀ > t_{(0,01; 4)},     t₂ > t_(0,01;4).

Принимаем нулевую гипотезу о значимости факторов  и  в уравнении (9.3.36).

Переходим к уравнению вида (9.3.31) с нецентрированными факторами:

                                               ,

т.е.

                    

или,  окончательно

                                                    .

▲