Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 3

Так как  является несмещённой оценкой , то ошибка

                                           ,                 (9.2.6)

представляет собой случайную величину с математическим ожиданием

                              

и дисперсией

                                              .

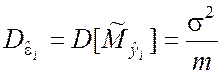4. Величины  и x_i являются стохастически независимыми, так как x_i являются детерминированными и, следовательно, справедливо равенство

                                               ,   ,

где  - корреляционный момент   и  x_i.

5. Результаты наблюдений являются независимыми:

                            ,   i ¹ l,   ,   .

6. Величины  и, следовательно, ошибки  распределены по нормальному закону. Необходимо заметить, что отклонения от нормального закона встречаются часто, однако имеют существенное значение только в том случае, если они велики.

В большинстве практических случаев сбор данных или весьма затруднён, или связан с большими затратами. Поэтому нередко каждому значению фактора x соответствует только одно значение результата и тогда  m = 1,  y_ij = y_i. В связи с тем, что это значение извлекается случайным образом из генеральной совокупности, величина y_i является несмещённой оценкой величины . Учитывая данное обстоятельство, имеем

                                 ,    ,   .

Регрессионный комплекс, соответствующий модели (9.2.2), значительно отличается от рассмотренного и имеет следующие особенности.

Пусть проводится исследование некоторой системы, при этом выполняется n опытов. В каждом опыте может быть зарегистрировано m значений фактора , характеризующего воздействие среды на систему, и столько же соответствующих значений результата , который является характеристикой воздействия системы на среду. Поскольку любая точка (x_ij; y_ij) случайным образом извлекается из генеральной совокупности, то её можно рассматривать как результат i-го опыта:

(x_ij; y_ij) = (x_i; y_i),    ,   .

В этом случае результаты наблюдений могут быть представлены в виде табл.9.2.

Таблица 9.2

Представление результатов однофакторного эксперимента (модель РА-2)

Значения фактора	x1	x1	×××	x1	×××	x1
Значения результата	y1	y1	×××	y1	×××	y1

Очевидно, что нижняя строка табл.9.2 представляет собой одновременно и оценки условных математических ожиданий:

                                    ,   .

Как и в модели РА-1 графически результаты наблюдений могут быть представлены в виде поля корреляции,  рис.9.3.

Рис.9.3. Поле корреляции и кривая регрессии

Из сравнения рис.9.2 и 9.3 вида разница между моделями РА-1 и РА-2. Если в первой модели результаты наблюдений рассеивались при определённых значениях фактора x, то во второй результаты располагаются произвольно по всему полю корреляции. Случайный характер значений фактора  определяет и особенности РА-2. Эти особенности проявляются как в системе предположений, в рамках которых выполняется РА-2, так и в методах, которые используются при его проведении. Для модели РА-2 справедливы предположения 2, 3, 5, 6.

Так как фактор является случайным, то в общем случае

                                                 ,

                             ,   .

Особенности методов, используемых в РА-2, рассмотрены ниже.

9.2.2. Построение уравнения регрессии

Пусть из каких-либо соображений выбран класс функций Y, которому принадлежит функция регрессии

                                                         y = f(x).                           (9.2.6)

Эта функция определяется также и вектором числовых параметров

                                            (a₀,  a₁,…, a_k)^т = A_<k+1>.              (9.2.7)

Поэтому выражение (9.2.6) можно представить в виде