Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 6

                                               H_0j: a_j ¹ 0,  

при соответствующих конкурирующих гипотезах H_1j: a_j = 0.

В качестве показателя согласованности при проверке гипотез H_0j используется выражение

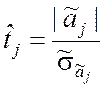                                              ,   ,               (9.2.27)

где  – модуль величины ;    – оценка среднего квадратического отклонения коэффициента .

Получение оценок  осуществляется так же, как это было описано в п.п.8.3.2. Здесь учтём специфику рассматриваемого вида функций регрессии (9.2.11) и уточним данную процедуру.

В соответствии с выражением (8.3.14) можно написать:

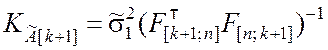                                       .       (9.2.28)

На главной диагонали корреляционной матрицы (9.2.28) вектора  будут дисперсии оценок коэффициентов регрессии:

                                         .         (9.2.29)

Случайная величина (9.2.27) подчинена закону распределения Стьюдента с   f = n – k – 1   степенями  свободы [1, 4]. Поэтому критерием правильности гипотез H_0j является выполнение неравенств

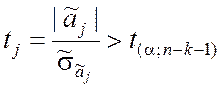                                       , ,        (9.2.30)

где t_j – наблюдаемое значение показателя согласованности гипотезы H_0j; t_{(a; n–k–1)} – критическое значение данного показателя при уровне значимости  a  и  f  степенях свободы.

Критическое значение t_{(a; n–k–1)} берётся из таблицы критических точек распределения Стьюдента (приложение 6). Очевидно, что входами в таблицу являются  a  и  f.

Коэффициенты регрессии, для которых не выполняется условие (9.2.30), принимаются равными нулю. Проверка неравенств (9.2.30) называется проверкой значимости коэффициентов регрессии по критерию Стьюдента.

Следует отметить, что при решении практических задач встречаются случаи, когда после исключения незначимых коэффициентов в соответствии с критерием Стьюдента регрессионная зависимость становится неадекватной. Такие случаи вызывают сомнения в универсальности этого широко применяемого в настоящее время критерия. Поэтому после исключения незначимых коэффициентов проверку адекватности уравнения регрессии по критерию Фишера целесообразно повторить.

9.2.5. Примеры однофакторного регрессионного анализа

Из вышеизложенного следует, что однофакторный регрессионный анализ проводится в следующей последовательности.

1. Выбирается вид функции регрессии.

2. Составляется система нормальных уравнений.

3. Находится решение системы нормальных уравнений (определяются оценки коэффициентов регрессии).

4. Проверяется адекватность построенного уравнения регрессии экспериментальным данным.

5. Проверяется значимость коэффициентов регрессии.

6. Повторно проверяется адекватность уравнения регрессии после исключения незначимых коэффициентов.

П р и м е р 9.1. Для исследования зависимости выходного сигнала y системы от входного воздействия x проведены испытания, результаты которых сведены в табл.9.3.

Необходимо построить уравнение регрессии y = f(x) в предположении, что оно является алгебраическим полиномом третьей степени. Расчёты произвести в скалярной форме.

Таблица 9.3

Массив экспериментальных данных

x	–2	–1	0	1	3
y	5	4	5	2	–39

▼ 1. Класс функций Y задан в условии задачи – это полиномы третьей степени

                                          y = a₀x³ + a₁x² + a₂x + a₃.           (9.2.31)

Они являются функциями вида (9.2.11). Для данного случая выражение (9.2.11) представляется как

                               y = a₀ f₀(x) + a₁ f₁(x) + a₂ f₂(x) + a₃ f₃(x), (9.2.32)

где f₀(x) = x³,   f₁(x) = x²,f₂(x) = x,   f₃(x) = 1.                                                        (9.2.33)

2. Для функции (9.2.32) и заданного количества опытов система нормальных уравнений (9.2.17) принимает вид