Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 9

        A₁₁ = 2716;         A₂₁ = –3780;     A₃₁ = –13384;     A₄₁ = 3696;

        A₁₂ = –3780;       A₂₂ = 8172;        A₃₂ = 15480;       A₄₂ = –13248;

        A₁₃ = –13384;     A₂₃ = 126304;    A₃₃ = 76576;       A₄₃ = –10896;

     A₁₄ = 3696;         A₂₄ = –13248;     A₃₄ = –10896;     A₄₄ = 49248.

Определитель указанной матрицы  || = 106848.

В результате получили обратную матрицу

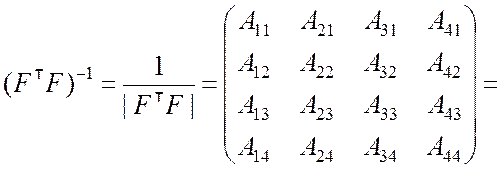
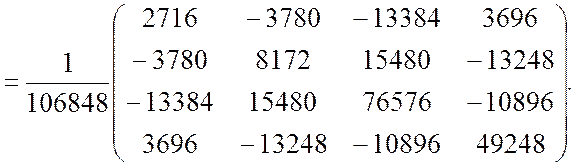
Далее вычисляем матрицу в правой части уравнения (9.2.39):

                      

   

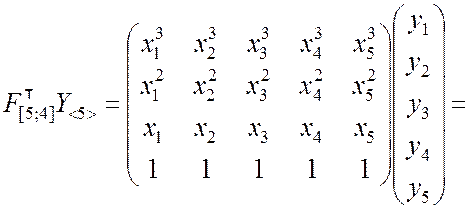
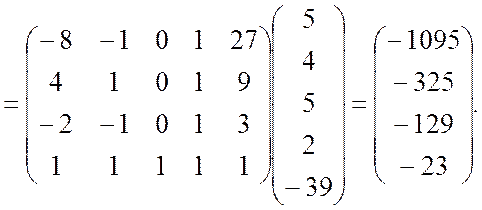
По формуле (9.2.40) находим оценки коэффициентов регрессии

                                              

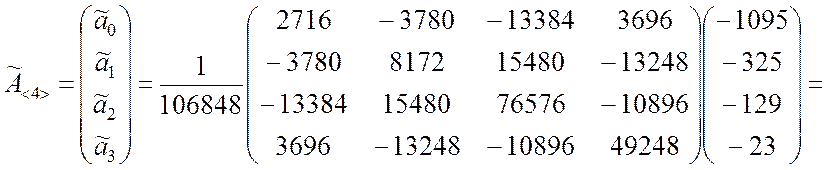
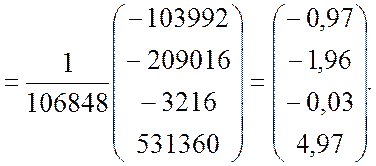
Так же, как и в примере 9.1 при расчётах в скалярной форме, получили уравнение регрессии

                                  .

Проверка адекватности уравнения экспериментальным данным и значимость коэффициентов регрессии выполняется аналогично тому, как это сделано в примере 9.1.

                                                                                                               ▲

9.3. Многофакторный линейный регрессионный анализ

9.3.1. Модели многофакторного линейного регрессионного анализа

В § 9.2 рассматривались модели однофакторного регрессионного анализа, линейные относительно коэффициентов регрессии. В то же время они могут быть нелинейными относительно независимой переменной (фактора), в примерах 9.1 и 9.2 рассматривалась именно такая нелинейная модель.

В настоящем подпараграфе рассмотрим модели многофакторного (множественного) регрессионного анализа, являющиеся линейными как относительно коэффициентов регрессии, так и относительно факторов.

Модель РА-1 определяется выражением

                                                          ,                            (9.3.1)

а модель РА-2 – выражением

                                                          .                             (9.3.2)

Условное математическое ожидание (9.1.1) результата наблюдения представляется как

                              .

Для модели РА-1 экспериментальные данные могут быть представлены табл.9.7.

Таблица 9.7

Представление результатов многофакторного эксперимента (модель РА-1)

Опыты	Факторы						Результаты наблюдений						Средние значения результатов наблюдений
	x1	x2	×××	xj	×××	xk	y1	y2	×××	ys	×××	ym
1	x11	x12	×××	x1j	×××	x1k	y11	y12	×××	y1s	×××	y1m
2	x21	x22	×××	x2j	×××	x2k	y21	y22	×××	y2s	×××	y2m
×××	×××	×××	×××	×××	×××	×××	×××	×××	×××	×××	×××	×××	×××
i	xi1	xi2	×××	xij	×××	xik	yi1	yi2	×××	yis	×××	yim
×××	×××	×××	×××	×××	×××	×××	×××	×××	×××	×××	×××	×××	×××
n	xn1	xn2	×××	xnj	×××	xnk	yn1	yn2	×××	yns	×××	ynm

В данной таблице значения факторов   X_<k>i,    являются фиксированными, что даёт возможность получить при данных значениях m результатов наблюдений. В частном случае может быть m = 1. При построении регрессионных зависимостей используется среднее значение результатов.