Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 12

Конкурирующие гипотезы состоят в предположении о равенстве нулю коэффициентов:

                                                      H_1j: b_j = 0.

В качестве показателя согласованности при проверке гипотез H_0j используется выражение

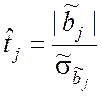                                               ,   ,               (9.3.21)

где || – модуль величины ;  – оценка среднего квадратического отклонения коэффициента .

Известно [1], что случайная величина (9.3.21) подчинена закону распределения Стьюдента.

Для того, чтобы выражение (9.3.21) можно было использовать практически, необходимо иметь методику вычисления величин . Она аналогична представленной в пп.9.2.4.

Рассматриваем корреляционную матрицу вектора :

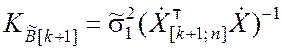                                          .           (9.3.22)

Элементы главной диагонали матрицы (9.3.22) и являются дисперсиями оценок коэффициентов регрессии:

                                         .

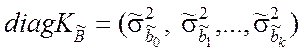Проверяются условия

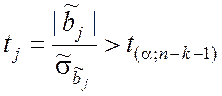                                      ,   ,       (9.3.23)

где t_j – вычисленное значение показателя согласованности гипотезы H_0j; t_{(a;n–k–1)} – критическое значение данного показателя при уровне значимости a    и    f₁ = n – k – 1    степенях свободы. Критическое значение t_{(a;n–k–1)}  берётся из таблицы критических точек распределения Стьюдента ( приложение 6).

Коэффициенты регрессии, для которых условие (9.3.23) не выполняется, принимаются равными нулю. Следовательно, соответствующие им факторы являются незначимыми. Проверка условий (9.3.23) называется селекцией факторов по критерию Стьюдента.

9.3.5. Пример многофакторного линейного регрессионного     анализа

Из вышеизложенного очевидно, что многофакторный линейный регрессионный анализ проводится в следующей последовательности.

1. Определяется количество слагаемых в линейной функции регрессии вида (9.3.1) или (9.3.2) в зависимости от числа факторов.

2. Выполняется центрирование факторов.

3. Составляется система нормальных уравнений.

4. Находится решение системы нормальных уравнений (определяются оценки коэффициентов регрессии).

5. Проверяется адекватность построенного уравнения регрессии экспериментальным данным.

6. Производится селекция факторов.

7. Повторно проверяется адекватность уравнения регрессии после исключения незначимых факторов.

П р и м е р 9.3. Для исследования зависимости выходного сигнала y системы от входного воздействия X_<2> = (x₁, x₂)^т, проведены испытания, результаты которых сведены в табл.9.9.

Необходимо построить регрессионную зависимость y от X_<2> в предположении, что она является линейным алгебраическим полиномом.

Таблица 9.9

Массив экспериментальных данных

x1	–0,5	0	0,8	0,4	0,5	0,6
x2	–3	–1	2	0,5	1,5	6
y	–15,1	–1	19,9	9,5	16,5	47,9

▼ 1. В рассматриваемой задаче функция регрессии представляет собой линейный алгебраический полином от двух независимых переменных

                                               y = b₀ + b₁x₁ + b₂x₂.

2. Составляем таблицу экспериментальных данных с центрированными значениями факторов.

Предварительно вычисляем средние значения факторов:

                    ;

                                                 ;

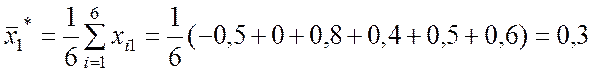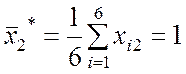Используя формулы (9.3.5), производим центрирование факторов, результаты заносятся в таб.9.10.

Таблица 9.10

Массив экспериментальных данных с центрированными значениями факторов

	–0,8	–0,3	0,5	0,1	0,2	0,3
	–4	–2	1	–0,5	0,5	5
y	–15,1	–1	19,9	9,5	16,5	47,9

Таким образом, вначале коэффициенты регрессии оцениваем в выражении функции (9.3.7), которая для данной задачи принимает вид