Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 7

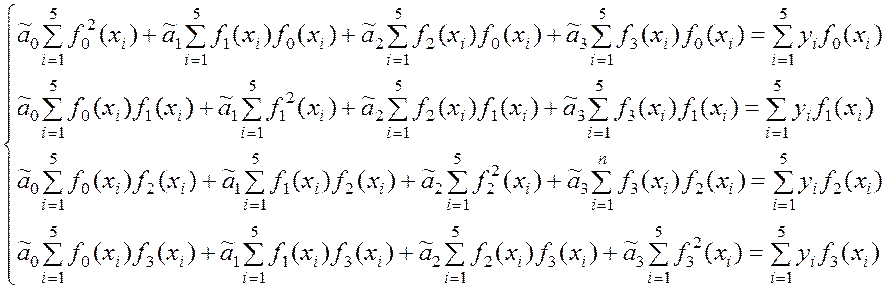
(9.2.34)

С учётом (9.2.33) система уравнений (9.2.34) преобразуется следующим образом:

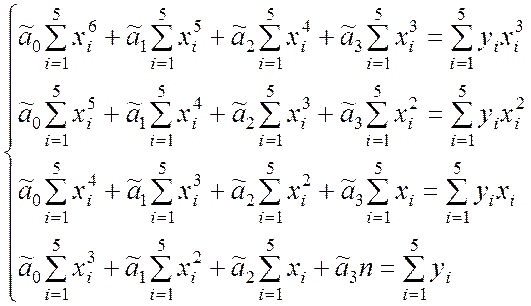                                                                                 (9.2.35)

3. Оценки коэффициентов уравнения регрессии (т.е. решение системы линейных уравнений (9.2.35)) находим по формулам   (9.2.18):

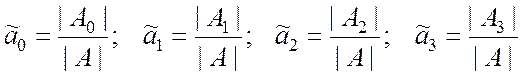                         .                                                        (9.2.36)

Развёрнутый вид определителей в соотношениях (9.2.36):

;                                      ;

;                                   ;

                                .

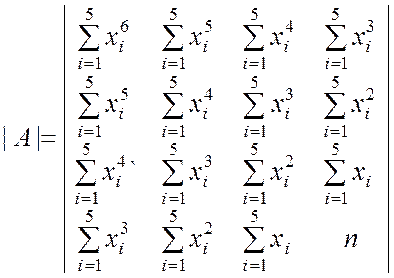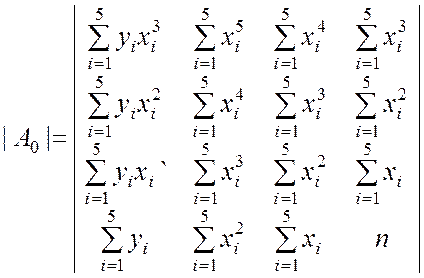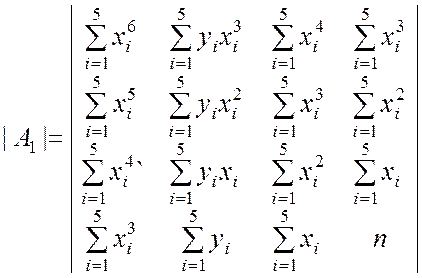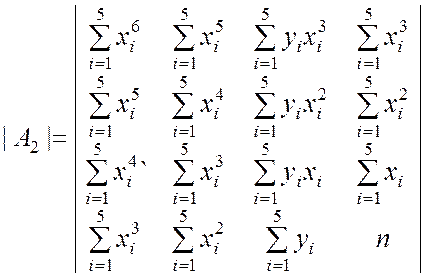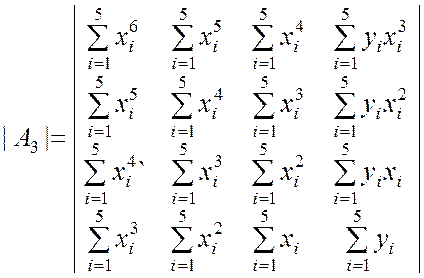Составляем расчётную таблицу 9.4 для вычисления коэффициентов системы линейных уравнений (9.2.35).

Таблица 9.4

Расчётная таблица

xi	yi
1	2	3	4	5	6	7	8	9	10
–2	5	4	–8	16	–32	64	–10	20	–40
–1	4	1	–1	1	–1	1	–4	4	–4
0	5	0	0	0	0	0	0	0	0
1	2	1	1	1	1	1	2	2	2
3	–39	9	27	81	243	729	–117	–351	–1053
= =1	= = –23	= =15	= =19	= =99	= =211	= =795	= = –129	= = –325	= = –1095

Получаем систему уравнений (9.2.35) с числовыми значениями коэффициентов при неизвестных:

                                           

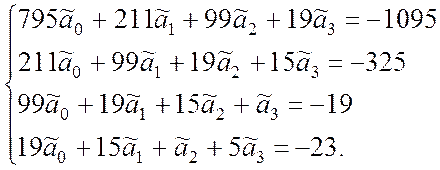
Определитель | A | четвёртого порядка вычисляем разложением по первой строке:

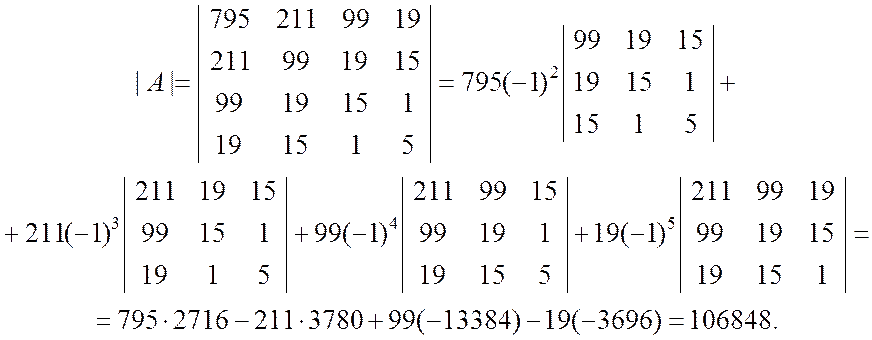
При разложении определителя | A | получены четыре определителя третьего порядка, которые вычисляем также разложением по первой строке:

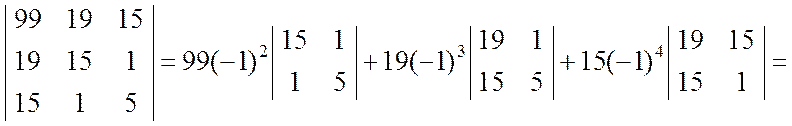
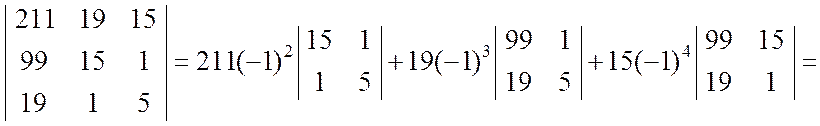
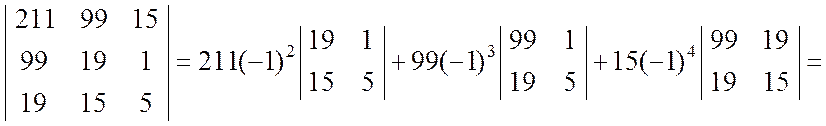
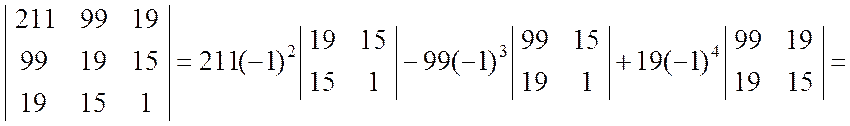
Аналогично находим

;

;

;

.

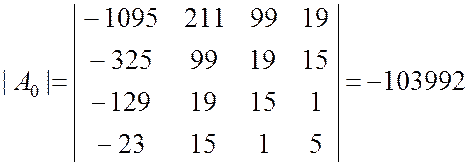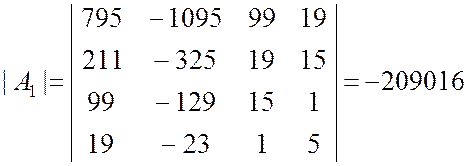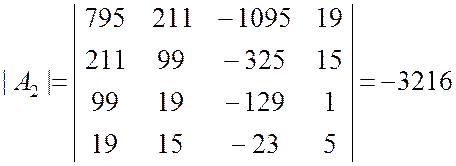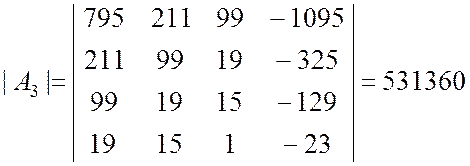По формулам (9.2.36) вычисляем оценки коэффициентов регрессии:

      

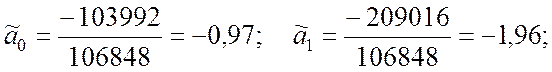
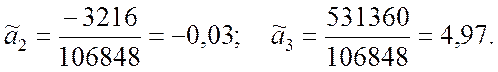
Получили уравнение регрессии

                                  .

4. Проверяем адекватность регрессионной зависимости экспериментальным данным. Для этого необходимо вычислить оценки дисперсий (9.2.25) и (9.2.26). Составляем табл.9.5.

Таблица 9.5

Расчётная таблица

xi	yi
–2	5	9,6	92,16	4,95	0,05	0,0025
–1	4	8,6	73,96	4,01	–0,01	0,0001
0	5	9,6	92,16	4,97	0,03	0,0009
1	2	6,6	43,56	2,01	–0,01	0,0001
3	–39	–34,4	1183	–38,95	–0,05	0,0025

Оценка математического ожидания выходной переменной y, которая используется при расчётах в табл.9.5, найдена по формуле (5.1.1):

                             .

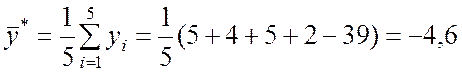Необходимые данные для вычисления оценок дисперсий s² и  берём из табл.9.5:

                                  ;

                                 .

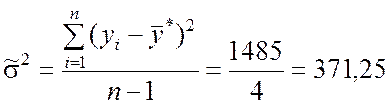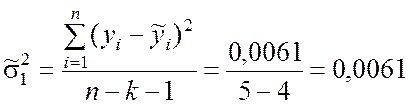Наблюдаемое значение показателя согласованности (9.2.23):

                                          .                      

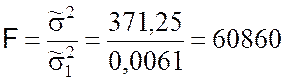Критическое значение показателя согласованности при уровне значимости a = 0,01 и степенях свободы   f₁ = n – 1 = 4,   f₂ = n – k – 1 = 1, находим в приложении 5:

                                                 F_{(0,01; 4; 1)} = 5625.