Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 4

                                   y = f(x;  a₀,  a₁,…, a_k) = f(x; A_<k+1>).     (9.2.8)

Построение уравнения регрессии сводится к решению задачи оценивания параметров (9.2.7), которые называются коэффициентами регрессии. Эта задача может быть решена на основе ряда принципов, являющихся базовыми для статистических методов обработки данных. В практике исследований наиболее широкое применение имеет подход, опирающийся на принцип максимального правдоподобия и, в частности, подход, использующий метод наименьших квадратов.

В соответствии с данным методом задача сводится к получению подходящей оценки  вектора A_<k+1>, минимизирующей сумму квадратов отклонений (невязок) наблюдаемых значений результата от выборочной функции регрессии. Указанные невязки представляются выражением

                                            ,   .               (9.2.9)

Следовательно, необходимо найти минимальное значение величины

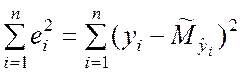                                             .             (9.2.10)

Рассмотрим только случай, когда функция регрессии (9.2.8) является линейной относительно оцениваемых параметров:

.

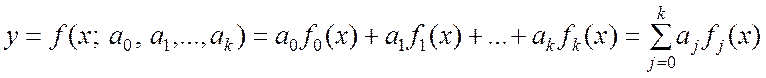                                                                                              (9.2.11)

Тогда оценки математических ожиданий результата определяются из выражения

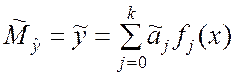                                             .              (9.2.12)

Принимая во внимание (9.2.12), соотношение (9.2.10) можно записать в виде

                                        .

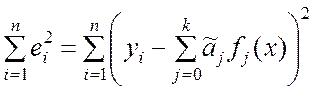Следовательно, оценки  должны быть таковы, чтобы выполнялось условие

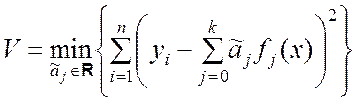                                     .     (9.2.13)

Из раздела 8 следует, что для нахождения минимума суммы квадратов невязок (9.2.13) необходимо составить систему нормальных уравнений вида (8.2.10). При условии, что используется функция регрессии (9.2.11), указанная система записывается следующим образом:

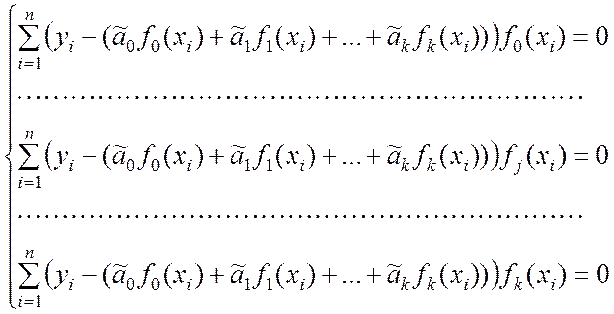                                                                           (9.2.14)

В уравнениях (9.2.14) учтено, что

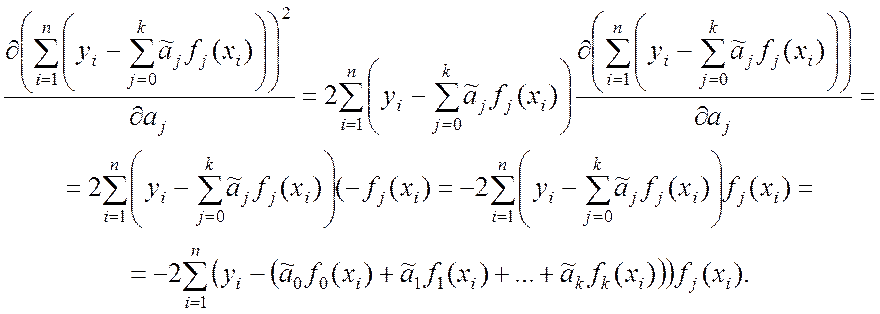
                                                                                              (9.2.15)

В выражении (9.2.15) использованы правила дифференцирования сложной функции многих переменных. Поскольку частная производная (9.2.15) приравнивается к нулю, имеем

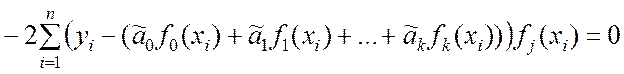                 .                                                        (9.2.16)

Обе части уравнения (9.2.16) умножаем на –2 и, таким образом, получаем j-е уравнение системы (9.2.14):

                   .

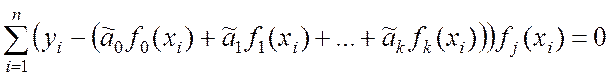Выполняем почленное суммирование в уравнениях (9.2.14), слагаемые, содержащие y_i переносим в правую часть, затем умножаем на –1 обе части каждого уравнения.

В результате получаем систему

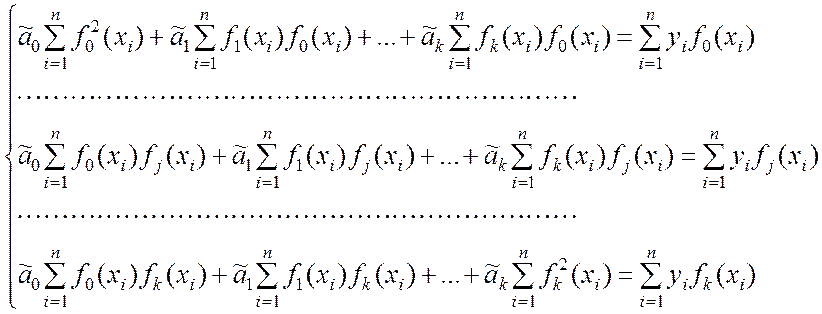
                                                                                              (9.2.17)

Уравнения (9.2.17) представляют собой систему линейных уравнений относительно оценок . Следовательно, она решается любым из методов решения систем таких уравнений.

Например, оценки коэффициентов регрессии могут быть найдены по формулам Крамера:

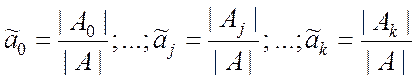                                 , (9.2.18)

где | A | – определитель коэффициентов при неизвестных системы (9.2.17); | A_j |,  – определители, которые формируются на основе определителя | A | путём замены j-го столбца столбцом свободных членов.

Таким образом, развёрнутый вид данных определителей будет следующим:

        ;

             ;

     ;

             .

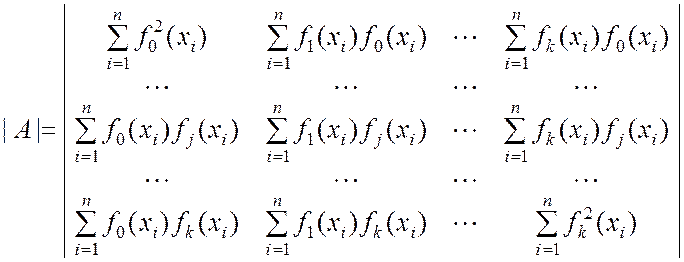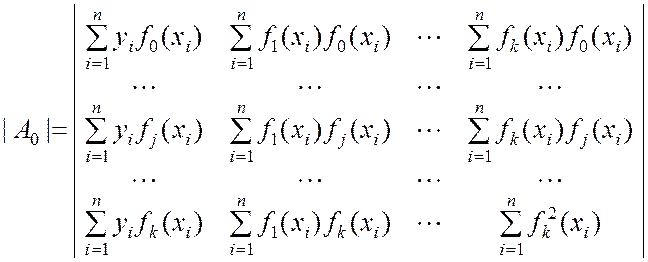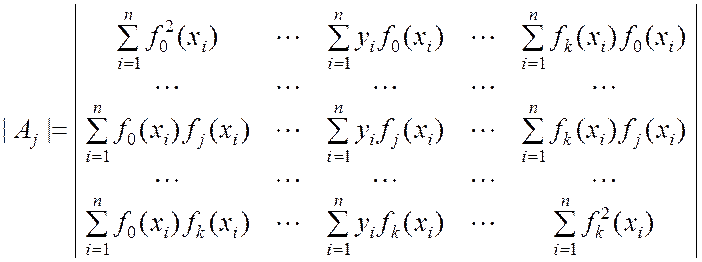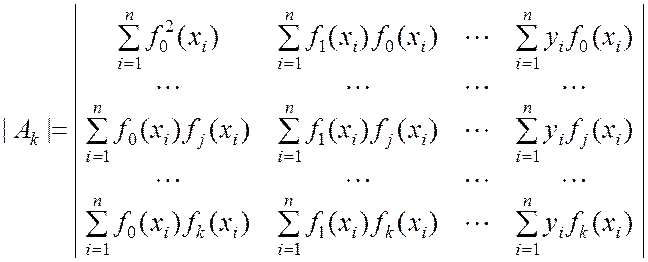Запишем систему уравнений (9.2.17) в матричной форме:

                                    ,    (9.2.19)

где                            ;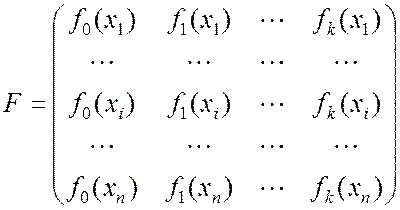

                             ;    .

Умножим слева обе части матричного уравнения (9.2.19) на квадратную матрицу :

                                    .

Далее учитываем, что

                                     ,    ,

где E = E_[k+1] – единичная матрица порядка  k+1.