Для модели РА-2 экспериментальные данные представляются
табл.9.8. В данной таблице имеют место системы случайных величин ![]() ,
, ![]() , т.е.
каждому сочетанию значений факторов
, т.е.
каждому сочетанию значений факторов ![]() соответствует одно
значение результата
соответствует одно
значение результата ![]() .
.
В рассматриваемом случае линейного регрессионного анализа методы построения моделей вида (9.3.1) и (9.3.2) одинаковы. Это связано с тем, что математические ожидания ошибок наблюдений равны нулю. Предположения, рассмотренные в п.п.9.2.1, остаются в силе.
Таблица 9.8
Представление результатов многофакторного эксперимента (модель РА-2)
|
Опыты |
Факторы |
Результаты наблюдений |
|||||
|
x1 |
x2 |
××× |
xj |
××× |
xk |
||
|
1 |
x11 |
x12 |
××× |
x1j |
××× |
x1k |
y1 |
|
2 |
x21 |
x22 |
××× |
x2j |
××× |
x2k |
y2 |
|
××× |
××× |
××× |
××× |
××× |
××× |
××× |
××× |
|
i |
xi1 |
xi2 |
××× |
xij |
××× |
xik |
yi |
|
××× |
××× |
××× |
××× |
××× |
××× |
××× |
××× |
|
n |
xn1 |
xn2 |
××× |
xnj |
××× |
xnk |
yn |
Задача построения уравнения регрессии сводится к оцениванию коэффициентов
![]() (9.3.3)
(9.3.3)
в выражении
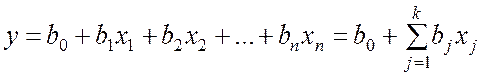 . (9.3.4)
. (9.3.4)
Поскольку значения факторов могут иметь различный порядок, то для упрощения вычислений целесообразно использовать их центрированные значения
![]() ,
, ![]() ,
, ![]() , (9.3.5)
, (9.3.5)
где 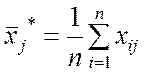 .
.
Кроме этого вводится n-мерный единичный вектор
![]() ,
,
что необходимо для оценки свободного члена уравнения регрессии. Матрица центрированных значений факторов при этом имеет вид
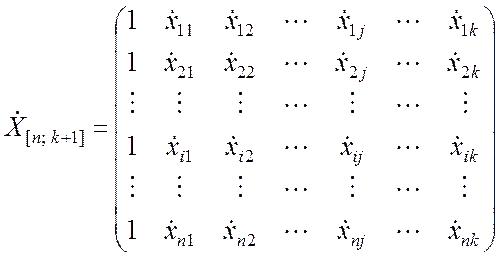 . (9.3.6)
. (9.3.6)
Из вышеизложенного следует, что коэффициенты регрессии оцениваются в уравнении
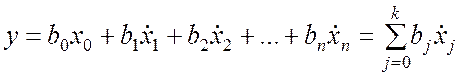 . (9.3.7)
. (9.3.7)
После вычисления данных оценок возврат к уравнению вида (9.3.4) осуществляется подстановкой (9.3.5). При этом значение коэффициента b0 изменяется.
Подходящую оценку ![]() вектора B<k+1> = (b0, b1,
b2,…,bk)т находим методом
наименьших квадратов. Так же, как и в случае однофакторной регрессии,
необходимо минимизировать сумму квадратов невязок (9.2.10). В данной формуле
оценки
вектора B<k+1> = (b0, b1,
b2,…,bk)т находим методом
наименьших квадратов. Так же, как и в случае однофакторной регрессии,
необходимо минимизировать сумму квадратов невязок (9.2.10). В данной формуле
оценки ![]() математических ожиданий результата
находятся из соотношения
математических ожиданий результата
находятся из соотношения
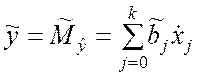 . (9.3.8)
. (9.3.8)
Учитывая (9.3.8), выражение (9.2.10) принимает вид
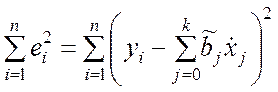 . (9.3.9)
. (9.3.9)
Таким образом, найденные оценки ![]() должны
удовлетворять условию
должны
удовлетворять условию
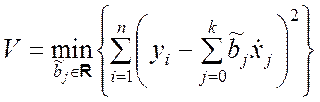 . (9.3.10)
. (9.3.10)
Для определения минимума (9.3.10) функции (9.3.9) составляем систему нормальных уравнений вида (8.2.10):
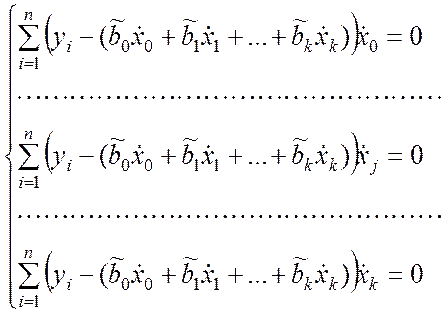 . (9.3.11)
. (9.3.11)
Уравнения (9.3.11) получены исходя из того, что частная
производная квадратичной функции (9.3.9) по переменной ![]() находится
следующим образом:
находится
следующим образом:
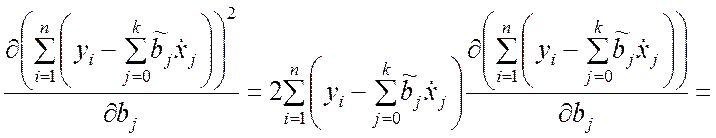
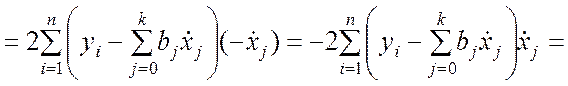 (9.3.12)
(9.3.12)
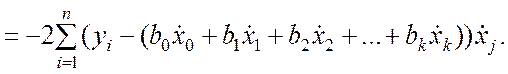
Частную производную (9.3.12) приравниваем к нулю и обе части полученного уравнения умножаем на –2. В результате имеем j-е уравнение системы (9.3.11). Далее выполняем почленное суммирование в уравнениях рассматриваемой системы, переносим в правую часть слагаемые, содержащие yi, а затем умножаем на –1 обе части каждого уравнения. Указанная последовательность операции приводит к эквивалентной системе уравнений
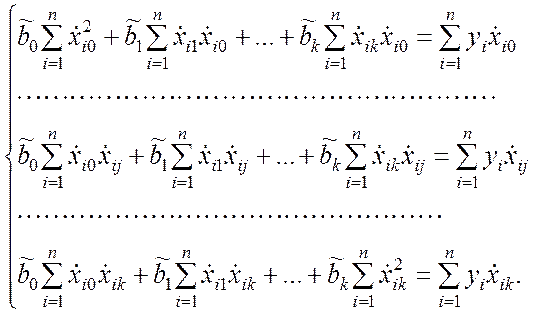
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.