Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 2

9.2.1. Модели однофакторного регрессионного комплекса

В однофакторном регрессионном анализе предполагается, что переменная  определяется только одной независимой переменной (одним фактором), следовательно, модели  РА-1  и  РА-2  имеют вид

                                             ,    

соответственно.

Данные модели могут быть представлены в несколько иной форме, а именно:

                                                    ,                       (9.2.1)

                                                 ,                    (9.2.2)

где  – ошибка результата наблюдения;  – ошибка наблюдаемого значения фактора.

В ряде источников модели однофакторного регрессионного анализа именуются моделями парной регрессии.

Регрессионный комплекс, соответствующий модели (9.2.1), описывается следующим образом. Пусть проводится исследование некоторой системы, при этом выполняется n опытов. В результате фиксируется n значений параметра x, характеризующего воздействие среды на систему. При каждом значении x_i,  данного параметра фиксируется m значений наблюдаемого признака , который характеризует воздействие системы на среду (рис.9.1). Результаты наблюдений могут быть представлены в виде табл.9.1.

Рис.9.1. Взаимодействие системы и среды

Таблица 9.1

Представление результатов однофакторного эксперимента (модель РА-1)

Значения фактора	Наблюдаемые значения результата
	1	2	×××	j	×××	m
x1	y11	y12	×××	y1j	×××	y1m
x2	y21	y22	×××	y2j	×××	y2m
×××	×××	×××	×××	×××	×××	×××	×××
xi	yi1	yi2	×××	yij	×××	yim
×××	×××	×××	×××	×××	×××	×××	×××
xn	yn1	yn2	×××	ynj	×××	ynm

В данной таблице кроме результатов наблюдений приведены оценки  условных математических ожиданий результатов наблюдений для различных значений фактора x.

Графически результаты наблюдений могут быть изображены в виде поля корреляции, показанного на рис.9.2.

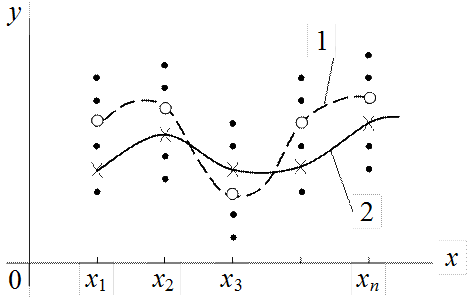
Рис.9.2. Поле корреляции и функции регрессии

На данном поле зачернённые точки соответствуют результатам наблюдений, крестики – значениям оценок математических ожиданий

                                        ,   ,

а кружки – значениям математических ожиданий

,   .

Предположим, что между  и x существует зависимость, которая может быть описана в виде

,   .

Тогда кривая, проведённая через значения  представляет собой функцию регрессии генеральной совокупности (кривая 1, рис.9.2). Так как каждая оценка  условного математического ожидания  представляет собой несмещённую оценку, то кривая 2, рис.9.2, проходящая через значения , будет одной из приемлемых оценок функции регрессии генеральной совокупности. Данная кривая называется выборочной функцией регрессии или оценкой функции регрессии.

Задачей регрессионного анализа является определение выборочной функции регрессии, наилучшим образом (в каком-либо смысле) соответствующей функции регрессии генеральной совокупности.

Для того чтобы данная задача была конструктивной, т.е. допускала решение, вводится ряд предположений, в рамках которых справедливо применение регрессионного анализа. Эти предположения состоят в следующем.

1. Величина x является неслучайной, т.е. задаётся или измеряется без ошибок.

2. Результаты наблюдений получены таким образом, что

                                    ,   , .       (9.2.3)

3. Для каждого x_i распределение величины  имеет постоянную дисперсию:

                                      ,   .         (9.2.4)

Учитывая (9.2.4), для любого y_i можно записать

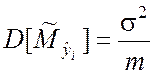                                            ,   .              (9.2.5)