Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 8

Очевидно, что неравенство (9.2.24) выполняется, т.е. F >F_{(0,01; 4; 1)}. Следовательно, нулевая гипотеза H₀ о соответствии функции регрессии вида (9.2.31) экспериментальным данным принимается.

5. Проверяем значимость коэффициентов уравнения регрессии.

Для вычисления наблюдаемых значений показателя согласованности (9.2.30) необходимо найти диагональные элементы корреляционной матрицы (9.2.28). В рассматриваемом примере матрица F представляется следующим образом:

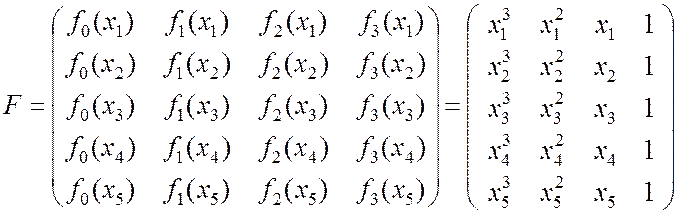         .                                                        (9.2.37)

Находим произведение транспонированной матрицы F на исходную:

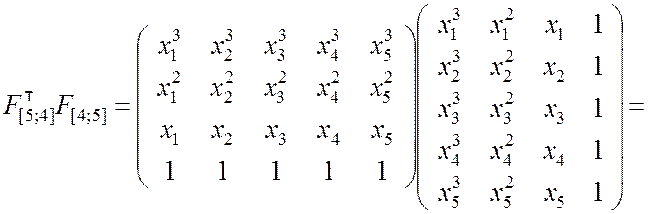
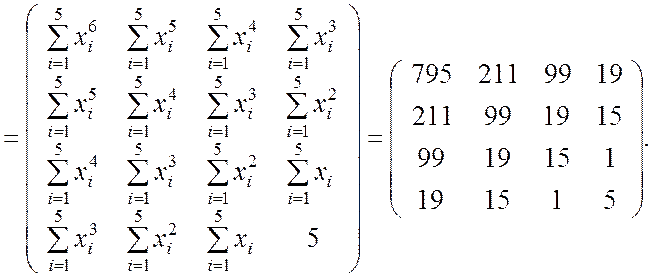                                                                      (9.2.38)

Далее требуется найти элементы главной диагонали матрицы :

                    ,

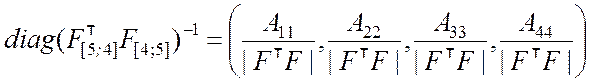где  – определитель матрицы ; A_ii,  – алгебраические дополнения элементов главной диагонали этой же матрицы.

Вычисляем определитель и алгебраические дополнения:

                              ;

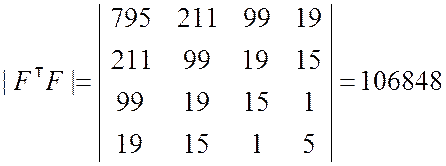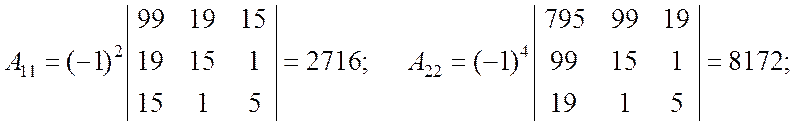
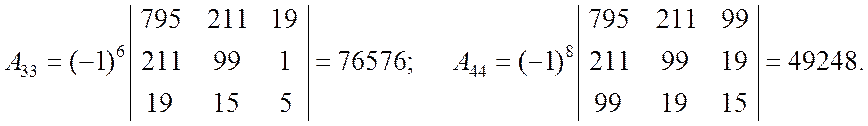
Таким образом, имеем

                

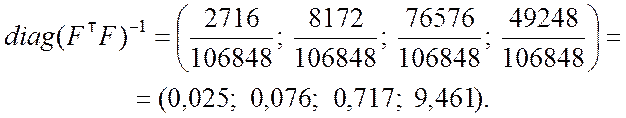
Главная диагональ (9.2.29) корреляционной матрицы вектора оценок коэффициентов регрессии:

.

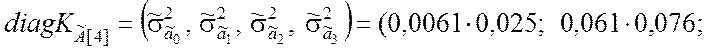
Вычисляем оценки средних квадратических отклонений коэффициентов   , :

                   ;     ;

                 ;     .

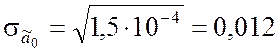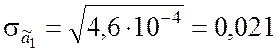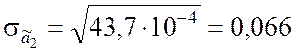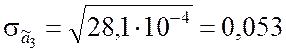Находим наблюдаемые значения показателя  (9.2.27):

.

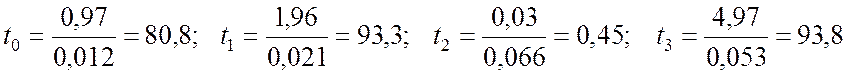Критическое значение показателя согласованности при уровне значимости a = 0,01 и одной степени свободы f = 1 находим в приложении 6: t_(0,01; 1) = 63,7.

Проверяем условие (9.2.30) и получаем:

                   t₀ > t_(0,01; 1);     t₁ > t_(0,01; 1);     t₂ < t_(0,01; 1);      t₃ > t_(0,01; 1).

На основе приведённых неравенств делаем вывод, что коэффициенты a₀, a₁ и a₃ являются значимыми, а коэффициент a₂ принимаем равным нулю.

Окончательный вид уравнения регрессии

                                        .

6. Проверяем адекватность последнего уравнения по критерию Фишера.  Составляем табл.9.6.

Таблица 9.6

Расчётная таблица

xi	yi
–2	5	4,89	0,11	0,0121
–1	4	3,98	0,02	0,0004
0	5	4,97	0,03	0,0009
1	2	2,04	–0,04	0,0016
3	–39	–38,86	–0,14	0,0196

Вычисляем оценку остаточной дисперсии с учётом результата, полученного в табл.9.6:

                                 .

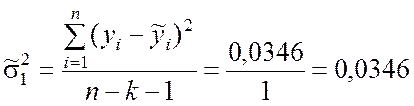Общая дисперсия остаётся прежней. Поэтому наблюдаемое значение показателя согласованности (9.2.33) будет следующим:

                                          .                      

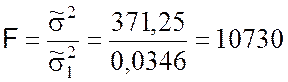Очевидно, что при критическом значении показателя согласованности F_{(0,01; 4; 1)} = 5625 неравенство (9.2.24) выполняется. Таким образом, повторная проверка адекватности по критерию Фишера подтверждает справедливость гипотезы о соответствии функции регрессии вида (9.2.31) экспериментальным данным.        

                                                                                                               ▲

П р и м е р 9.2. В условиях примера 9.1 построить уравнение регрессии, но расчёты произвести в матричной форме.

▼ Матричное уравнение (9.2.19) для рассматриваемого примера имеет вид

                                     ,     (9.2.39)

где матрицы F и  представлены выражениями (9.2.37), (9.2.38) соответственно;

                                           ;   .

Выражение (9.2.20) для вычисления оценок коэффициентов регрессии представляется в виде

                                       .        (9.2.40)

Вычисляем обратную матрицу  для матрицы

                                   .

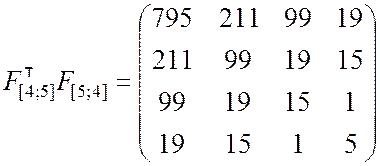Алгебраические дополнения элементов матрицы :