Методы регрессионного анализа. Сущность и задачи регрессионного анализа (Раздел 9 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 13

                                                                (9.3.24)

3. Система нормальных уравнений представляется следующим образом:

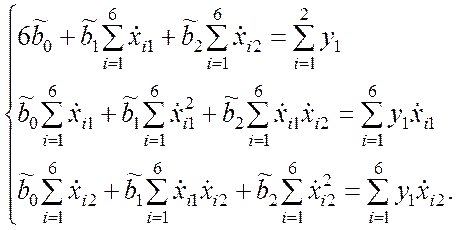                                                                                      (9.3.25)

4. Представим и решим систему (9.3.25) в матричной форме.

Матричное уравнение, эквивалентное данной системе, принимает вид

                                        ,        (9.3.26)

где                         ;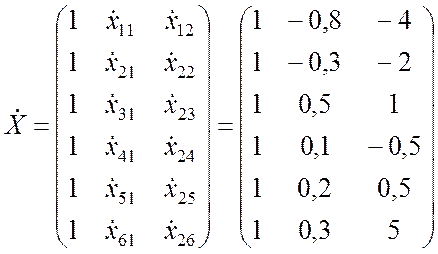

;   .

Выражение (9.3.16) для вычисления оценок коэффициентов регрессии представляется равенством

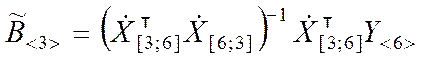                                . (9.3.27)

Вычисляем матрицу  :

  

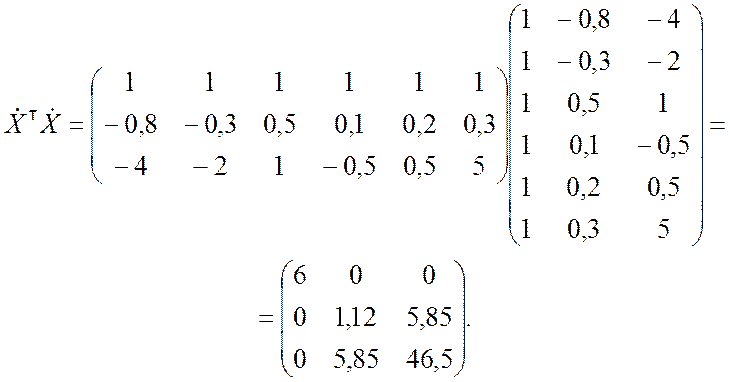
Для полученной матрицы находим обратную матрицу:

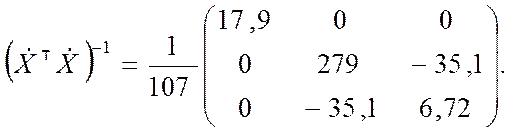                                                                                  (9.3.28)

Далее находим матрицу в правой части уравнения (9.3.26):

      

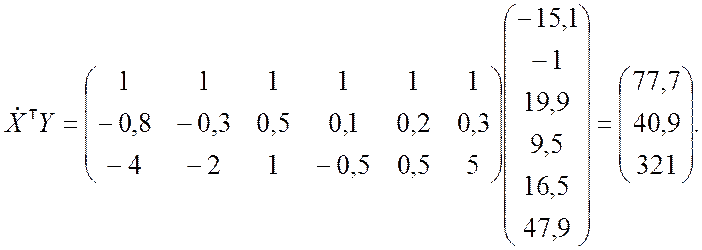
По формуле (9.3.27) вычисляем оценку вектора коэффициентов регрессии

                        .

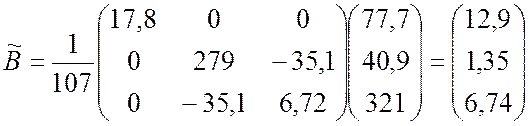Получим следующее уравнение регрессии:

                                          .          (9.3.29)

5. Проверяем адекватность уравнения (9.3.29) экспериментальным данным.

Предварительно вычисляем оценки дисперсий (9.3.18) и (9.3.19). Для этого составляем табл.9.11.

Таблица 9.11

Расчётная таблица

		yi
–0,8	–4	–15,1	–28	784	–15,2	0,01	0,0001
–0,3	–2	–1	–13,9	193	–0,98	–0,02	0,0004
0,5	1	19,9	7	49	20,3	–0,40	0,16
0,1	–0,5	9,5	–3,4	11,6	9,66	0,16	0,0256
0,2	0,5	16,5	3,6	13	16,6	–0,10	0,01
0,3	5	47,9	35	1225	47	0,90	0,81

Оценка математического ожидания выходной переменной y, используемая при расчётах в табл.9.11, найдена по формуле (5.1.1):

              .

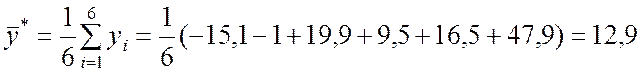Необходимые данные для вычисления оценок дисперсий  берём из табл.9.11:

                                     ,                 

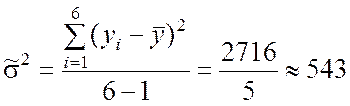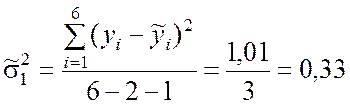                                     ,      (9.3.30)

Наблюдаемое значение показателя согласованности (9.3.17):

                                            

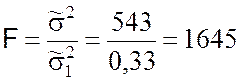
Для отыскания критического значения показателя согласованности при  уровне  значимости   a = 0,01   и  степенях  свободы  f₁ = n – 1 = 5,    f₂ = n – k – 1 = 3   используем приложение 5 и получаем F_(0,01;5;3) = 28,24.

Поскольку неравенство (9.3.20) выполняется (F > F_(0,01;5;3)), нулевую гипотезу об адекватности функции регрессии вида (9.3.24) экспериментальным данным принимаем.

6. Выполняем селекцию факторов. Для этого находим элементы главной диагонали корреляционной матрицы (9.3.22). Учитывая выражения (9.3.28) и (9.3.30), имеем

                       .

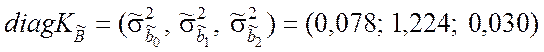Оценки средних квадратических отклонений коэффициентов ,  принимают значения:

                          ;       ;     .

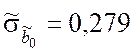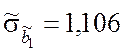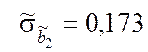Для каждого фактора находим наблюдаемое значение показателя согласованности (9.3.21):

 .

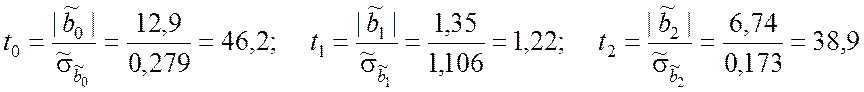Для числа степеней свободы  f = n – k –1 = 3  и уровня значимости a = 0,01 критическое значение показателя согласованности t_(0,01;3) = 5,84. Следовательно,

                               t₀ > t_(0,01;3),      t₁ < t_(0,01;3),      t₃ > t_(0,01;3).

В отношении фактора  принимаем конкурирующую гипотезу о его незначимости. Тогда в правой части выражения (9.3.24) второе слагаемое приравниваем к нулю. Поскольку в исходной матрице  исключается второй столбец, оценки коэффициентов регрессии b₀ и b₂ необходимо пересчитать.