Одной из важнейших задач обработки данных является задача оценивания (экспериментального определения) вероятностных характеристик случайных объектов.
Пусть ![]() – случайная величина,
характеризующая свойство исследуемого объекта. Требуется на основе случайной
выборки
– случайная величина,
характеризующая свойство исследуемого объекта. Требуется на основе случайной
выборки ![]() ,
, ![]() ,…,
,…,![]() выработать объективное суждение о
вероятностных свойствах случайной величины
выработать объективное суждение о
вероятностных свойствах случайной величины ![]() .
.
Как было указано в § 1.3, любая функция случайной выборки
![]() (3.1.1)
(3.1.1)
называется статистикой. Если статистика (3.1.1) используется в качестве приближения неизвестной вероятностной характеристики (закона или параметра распределения) случайной величины, то её значение
![]() , (3.1.2)
, (3.1.2)
полученное в результате обработки экспериментальных данных по формуле (3.1.2), называется оценкой этой характеристики.
Известно, что исчерпывающей характеристикой вероятностного поведения
случайной величины ![]() является закон её распределения
является закон её распределения ![]() или
или ![]() .
Поэтому основной целью в рассматриваемой здесь задаче является построение
закона распределения случайной величины
.
Поэтому основной целью в рассматриваемой здесь задаче является построение
закона распределения случайной величины ![]() по экспериментальным
данным, т.е. его представление как функции выборки
по экспериментальным
данным, т.е. его представление как функции выборки
![]() ,
,
которая может служить в качестве оценки функции ![]() , обладающей требуемой точностью и
надёжностью (достоверностью).
, обладающей требуемой точностью и
надёжностью (достоверностью).
В общем случае функция ![]() зависит
как от своего аргумента, так и от параметров распределения:
зависит
как от своего аргумента, так и от параметров распределения:
![]() .
.
Параметрическая обработка данных опирается на предположение
о том, что класс распределений, которому принадлежит функция ![]() , априорно известен. Конкретные значения
параметров A<m> этого распределения, выделяющие
его в рассматриваемом классе, неизвестны. Тогда оценивание функции
, априорно известен. Конкретные значения
параметров A<m> этого распределения, выделяющие
его в рассматриваемом классе, неизвестны. Тогда оценивание функции ![]() сводится к оцениванию её параметров A<m>,
т.е. к отысканию такой статистики
сводится к оцениванию её параметров A<m>,
т.е. к отысканию такой статистики
![]() ,
,
которая обеспечивала бы приближённое равенство
![]() .
.
Поскольку вся информация об исследуемом объекте содержится в выборке объёма n, то для однозначного решения задачи статистического оценивания m параметров требуется выполнение условия n > m.
В качестве критериев оценивания истинных значений характеристик используются соотношения следующего вида:
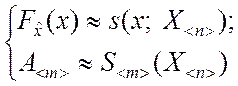 . (3.1.3)
. (3.1.3)
или
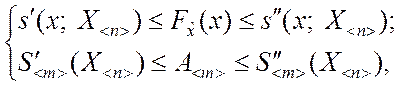 (3.1.4)
(3.1.4)
где ![]() ,
, ![]() –
нижняя и верхняя границы интервалов;
–
нижняя и верхняя границы интервалов; ![]() ,
, ![]() – границы m-мерных
областей.
– границы m-мерных
областей.
Оценивание вероятностных характеристик в соответствии с критерием (3.1.3) называется точечным, а в соответствии с критерием (3.1.4) – интервальным. Строго говоря оценки всегда являются точечными. Что же касается интервальных оценок, то их назначение - характеризовать качество точечных оценок.
Предположим, что распределение ![]() однопараметрическое,
т.е. A<m> = A<1> = a. Принятое
допущение позволяет существенно повысить наглядность рассуждений, которые без
затруднений распространяются на случай многопараметрического распределения.
Кроме того, будем считать, что класс распределений, которому принадлежит
функция
однопараметрическое,
т.е. A<m> = A<1> = a. Принятое
допущение позволяет существенно повысить наглядность рассуждений, которые без
затруднений распространяются на случай многопараметрического распределения.
Кроме того, будем считать, что класс распределений, которому принадлежит
функция ![]() , известно, но неизвестно значение
параметра a. В этом случае задача оценивания
функции распределения
, известно, но неизвестно значение
параметра a. В этом случае задача оценивания
функции распределения ![]() сводится к оцениванию параметра,
т.е. к определению соотношения вида
сводится к оцениванию параметра,
т.е. к определению соотношения вида
![]() ,
,
где ![]() – оценка параметра a.
– оценка параметра a.
Поскольку результаты ![]() наблюдений
над случайной величиной
наблюдений
над случайной величиной ![]() априори являются случайными,
то случайной оказывается и оценка
априори являются случайными,
то случайной оказывается и оценка ![]() :
:
![]() .
.
В общем случае ![]() ¹ a,
следовательно, и после получения оценки
¹ a,
следовательно, и после получения оценки ![]() параметра
a его неопределённость для исследователя полностью
не снимается. В то же время исследователь даёт вероятностное суждение об истинном
значении a согласно результату эксперимента так,
чтобы соответствовать ему наилучшим (в некотором смысле) образом. Оценка будет
объективной характеристикой параметра, если она удовлетворяет требованиям
несмещённости, состоятельности и эффективности.
параметра
a его неопределённость для исследователя полностью
не снимается. В то же время исследователь даёт вероятностное суждение об истинном
значении a согласно результату эксперимента так,
чтобы соответствовать ему наилучшим (в некотором смысле) образом. Оценка будет
объективной характеристикой параметра, если она удовлетворяет требованиям
несмещённости, состоятельности и эффективности.
Оценка ![]() параметра a называется несмещённой, если её математическое
ожидание равно оцениваемому параметру:
параметра a называется несмещённой, если её математическое
ожидание равно оцениваемому параметру:
![]() . (3.1.5)
. (3.1.5)
Если ![]() , то оценка называется смещённой.
, то оценка называется смещённой.
Оценка ![]() параметра a называется состоятельной, если она сходится
по вероятности к оцениваемому параметру:
параметра a называется состоятельной, если она сходится
по вероятности к оцениваемому параметру:
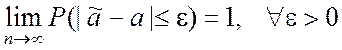 , (3.1.6)
, (3.1.6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.