Методы статистического оценивания. Постановка задачи оценивания законов и параметров распределения случайных величин (Раздел 3 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 4

                                           ,                       

где ;  .

Поскольку выборка  априори случайна, то и статистики ,, а следовательно, и доверительные границы ,  априори случайны:

                                     ;  .                 

При анализе качества статистических оценок вся информация об исследуемой переменной содержится в случайной выборке . Поэтому не только оценка  параметра, но и её максимальная вероятная погрешность e_b определяется через выборку:

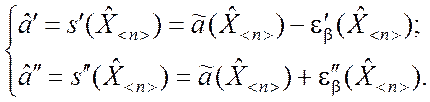                                   (3.2.4)

Соотношения (3.2.4) носят общий характер и в явном виде никогда не формируются. На практике погрешность e_b оценки  выражается через саму оценку:

                                                      .                                  

Таким образом, доверительные границы ,  для параметра a определяются его оценкой :

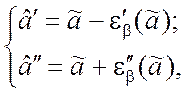                                                                     (3.2.5)

где функции  и  в общем случае различные. Соотношения (3.2.5) иллюстрируются рис.3.1.

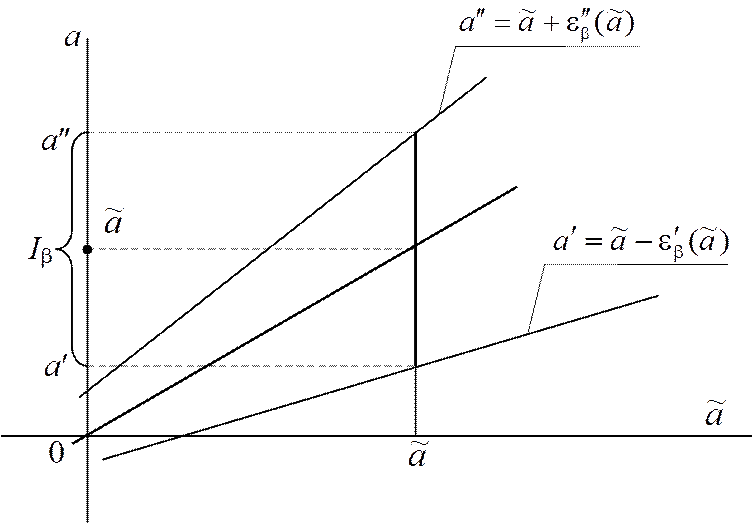
Рис.3.1. Зависимость доверительных границ параметра от его оценки

Выражения (3.2.1) и (3.2.2) были получены в предположении, что оценка  имеет симметричное относительно параметра a распределение. При этом доверительный интервал  оказывается также симметричным. В этом случае должны выполняться условия , которые означают равенство положительной и отрицательной максимальных вероятных погрешностей. В общем случае это требование не обязательно и при определении  и  в основу могут быть положены различные соображения. Чаще всего выдвигается требование

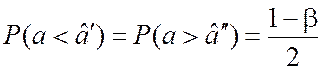                                       ,          (3.2.6)

означающее, что истинное значение a оцениваемого параметра может оказаться левее или правее его доверительного интервала с одинаковой вероятностью.

При условии (3.2.6) и симметричном распределении оценки  доверительный интервал для параметра  a  будет симметричным:

                                    .                

Следовательно, имеют место равенства

.                                                        (3.2.7)

Если распределение оценки  не симметрично относительно оцениваемого параметра a, то при условии (3.2.6) доверительный интервал не симметричен, и соотношение (3.2.7) принимает вид

                             ,         

где  и  – соответственно абсолютные значения максимальных с вероятностью b отрицательной и положительной погрешностей оценки  параметра a.

Итак, доверительный интервал (его составляющие  и ) характеризует точность, доверительная вероятность b – надёжность (достоверность) оценки , а вместе они определяют качество оценивания параметра a.

В § 3.1 отмечалось, что с ростом объёма n выборки оценка  сходится по вероятности к оцениваемому параметру a (закон больших чисел) и при этом её дисперсия стремится к нулю. Это значит, что с увеличением n растёт как точность, так и надёжность оценивания. В результате оказываются связанными между собой три характеристики качества статического оценивания:

-  доверительный интервал I_b,n(a);

-  доверительная вероятность b_e,n(a);

-  объём n_b,e(a) выборки, потребный для оценивания параметра a с заданной точностью и надёжностью.

Указанные характеристики связаны соотношениями, позволяющими управлять качеством статистического оценивания[2]

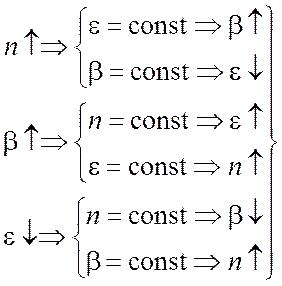                                                        (3.2.8)

Таким образом, при исследовании качества статистического оценивания решается одна из трёх основных задач:

-  определение доверительного интервала I_b,n (или половины его длины e_b,n)  для параметра a при заданной доверительной вероятности b и фиксированном объёме n выборки;