В выражении (3.3.6) величина tb - квантиль нормированного нормального распределения:
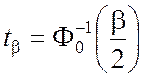 или
или 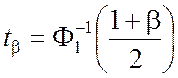 .
.
Значения функции tb приведены в приложении 4.
Если необходимые точность e и надёжность b заданы, то потребное для их обеспечения число nb,n испытаний находится из уравнения (3.3.6):
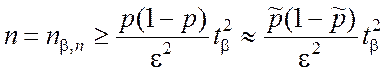 , (3.3.8)
, (3.3.8)
Формулы (3.3.5) – (3.3.8) определяют решения трёх основных задач исследования качества статистического оценивания (см. § 3.2) применительно к оценке вероятности случайного события по его частоте в серии n независимых однородных испытаний.
Из соотношения (3.3.8) видно, что потребный объём выборки обратно
пропорционален квадрату максимальной вероятной погрешности e оценки ![]() и
пропорционален квадрату функции tb, который растёт быстрее,
чем b. Поэтому для
оценивания вероятности случайного события по его частоте с достаточной
точностью и надёжностью требуется проведение довольно длинной серии испытаний.
Сказанное иллюстрируется табл.3.1, в которой приведены потребные числа n0,95;e испытаний, обеспечивающие с доверительной вероятностью b = 0,95
необходимую точность e
оценивания различных значений вероятности p.
и
пропорционален квадрату функции tb, который растёт быстрее,
чем b. Поэтому для
оценивания вероятности случайного события по его частоте с достаточной
точностью и надёжностью требуется проведение довольно длинной серии испытаний.
Сказанное иллюстрируется табл.3.1, в которой приведены потребные числа n0,95;e испытаний, обеспечивающие с доверительной вероятностью b = 0,95
необходимую точность e
оценивания различных значений вероятности p.
Таблица 3.1
Зависимость числа испытаний от требуемой доверительной вероятности
|
e |
р |
||||
|
0,9 |
0,8 |
0,7 |
0,6 |
0,5 |
|
|
0,05 |
139 |
246 |
323 |
369 |
385 |
|
0,01 |
3458 |
6147 |
8068 |
9220 |
9604 |
Из табл.3.1 видно, что потребное число nb;e испытаний растёт не только с
увеличением неоходимой точности оценивания, но и с приближением истинного
значения p оцениваемой вероятности к 0,5. Это
объяснимо, поскольку при p = 0,5 дисперсия оценки ![]() = p* достигает максимального значения, равного
0,25/n [см. формулу
(3.3.3)]. Указанный факт используется для определения верхней границы
потребного числа испытаний. Так, полагая p = 0,5, b = 0,95, имеем значение tb = t0,95 =1,96 » 2
(см. приложение 4). В соответствии с выражением (3.3.8) получаем
= p* достигает максимального значения, равного
0,25/n [см. формулу
(3.3.3)]. Указанный факт используется для определения верхней границы
потребного числа испытаний. Так, полагая p = 0,5, b = 0,95, имеем значение tb = t0,95 =1,96 » 2
(см. приложение 4). В соответствии с выражением (3.3.8) получаем
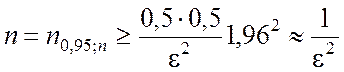 . (3.3.9)
. (3.3.9)
Пример 3.1. В процессе эксперимента выполнено 200 опытов, частота события A оказалась p* = 0,34.
1. Построить 85%-й доверительный интервал для вероятности события A.
2. Найти доверительную вероятность b для вероятности события A, если максимальная вероятная погрешность eb = 0,1.
▼ 1) Для b = 0,85 в приложении 4 находим tb = 1,439. Тогда по формуле (3.3.6) оценка максимальной вероятной ошибки составит
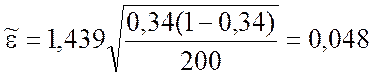 .
.
Находим доверительный интервал из соотношения (3.3.7)
I0,85; 200 » [0,34 – 0,048; 0,34 + 0,048] = [0,292; 0,388].
2) По формуле (3.3.5) находим доверительную вероятность
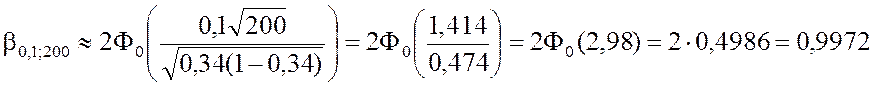 .
.
Значение функции Ф0(x) взято из приложения 2.
▲
Пример 3.2. В процессе эксперимента выполняются опыты, частота события составляет p* = 0,7.
1. Определить потребный объём выборки, чтобы максимальная вероятная погрешность оценки p* составляла e £ 0,05 при доверительной вероятности b =0,9.
2. Найти верхнюю границу потребного числа опытов при любой частоте события .
▼ 1) По заданному b находим tb = 1,643. Тогда в соответствии с формулой (3.3.8) потребный объём выборки составит
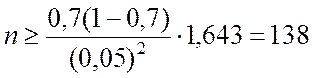 .
.
2) Из выражения (3.3.9) имеем
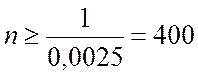 .
.
▲
[1] Для смещённой оценки понятие эффективности не определено.
[2] Символы , ¯ означают соответственно возрастание и убывание.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.