Если некоторое количество вещества М в начальный момент времени сосредоточено в начале сферической системы координат в другом веществе, в котором оно может диффундировать, то в последующие моменты времени его концентрация в различных точках основной среды будет описываться решением уравнения диффузии аналогичным уравнению (13.4.30).
Это решение, как указывалось выше, имеет вид:
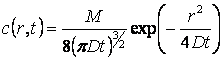 .
.
Очевидно, время релаксации концентрации будет равно:
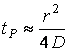 . (13.4.32)
. (13.4.32)
Пользуясь последним соотношением можно оценить время релаксации магнитного поля в неподвижное вещество. Предположим, что внутри земли возникло каким-либо образом некоторое магнитное поле. Тогда время в течение, которого это поле достигает поверхности земли можно оценить по формуле (13.4.32):
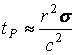 .
.
Если бы земля имела проводимость равную проводимости меди, то из последней формулы мы имели бы:
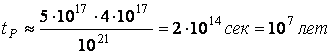
Для медного шара радиусом 100 см, имеем:
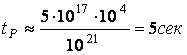
![]()
Рассмотрим установившееся движение проводящей
несжимаемой жидкости между двумя параллельными бесконечными пластинами в
перпендикулярном магнитном поле напряженностью ![]() .
Будем полагать, что движение вызывается градиентом давления направленным вдоль
пластин (рис.6.).
.
Будем полагать, что движение вызывается градиентом давления направленным вдоль
пластин (рис.6.).
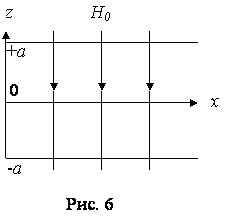
Пусть расстояние между пластинами равно 2а. Движение жидкости должно подчиняться следующим уравнениям:
1.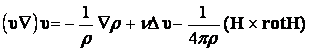 ,
,
2.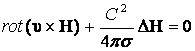 ,
(13.4.33)
,
(13.4.33)
3.![]() ,
, ![]() .
.
Будем полагать, что скорость жидкости направлена вдоль
пластин и зависит лишь от координаты ![]() :
:
![]() ,
, ![]() ,
, ![]() .
.
В силу бесконечности пластин в направлении осей X и Y очевидно напряженность магнитного поля может зависеть только от координаты Z. Тогда задача может рассматриваться как плоская.
![]() ,
, ![]() ,
, ![]() .
.
Спроектируем уравнение движения на оси координат:
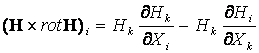 ,
,
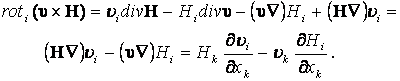
Проектируя на оси X,Y,Z ![]() с
учетом топологии движения получаем:
с
учетом топологии движения получаем:
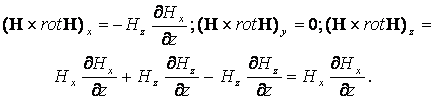
Для проекций ![]() получаем:
получаем:
![]() ,
, ![]() ,
, ![]() .
.
Таким образом, имеем следующую систему уравнений:
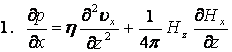 ,
,
2. 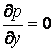 ,
,
3. 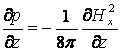 ,
,
4. 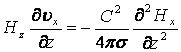 , (13.4.34)
, (13.4.34)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.