Механика \ Механика сплошных сред

Магнитная гидродинамика, страница 10

5.  0=0,

6.  ,

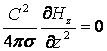7.  0=0,

8.  .

Решение системы проведем следующим образом: Из уравнения 8 системы (13.4.34) имеем:

 ,    .                            (13.4.35)

Тогда уравнение 6 системы (13.4.34) удовлетворяется тождественно. Из уравнения 2 системы (13.4.34) следует:

 .

Из уравнения 3 системы (13.4.34) имеем:

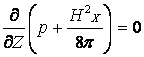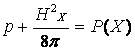 ,     .                              (13.4.36)

Далее дифференцируем уравнение 1 системы (13.4.34) по Z:

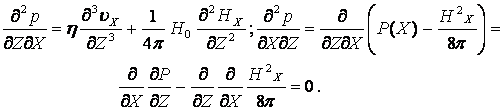
Поэтому с учетом (13.4.35), (13.4.36), (13.4.37) и 4 уравнения (13.4.34) 1 уравнение (13.4.34) имеет вид:

 .

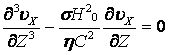Последнее уравнение можно записать следующим образом:

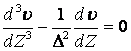
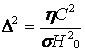  .                  (13.4.37)

Решение  уравнения (13.4.37) имеет вид:

 ,

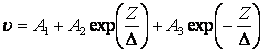 .                    (13.4.38)

Постоянные  могут быть найдены из граничных условий:

 ,     ,                  ,                  .

Подставляя в решение (13.4.38), имеем систему уравнений для нахождения постоянных :

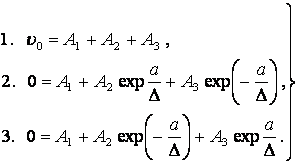               (13.4.39)

Из уравнений 2, 3 системы (13.4.39) имеем:

.

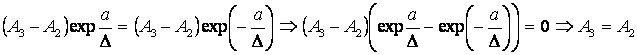Тогда уравнения 1, 2 системы (13.4.39) можно записать следующим образом:

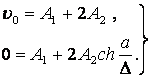                          (13.4.40)

Из (13.4.40) имеем:

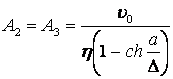 ,           .            (13.4.41)

Таким образом окончательно решение имеет вид:

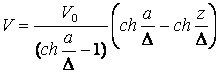 .                   (13.4.42)

Для нахождения Нх проинтегрируем один раз уравнение 4 (13.4.34):

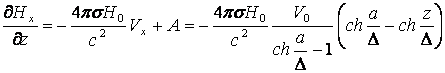 .   (13.4.43)

В выражении (13.4.43) постоянная A не зависит от z. Но т.к. Нх не зависит от х то А не должна зависеть от координаты х. Т.е. постоянная А не зависит от координат. Обозначая коэффициент перед квадратичными скобками в (13.4.43) через a в результате интегрирования (13.4.43) имеем:

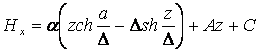 .                     (13.4.44)

Поскольку на границе z=±a нет ни каких поверхностных токов проводимости, то при z=±a должна быть непрерывна тангенциальная составляющая напряженности магнитного поля. Кроме того из симметрии задачи ясно, что Нх=0 при z=0.

Таким образом напряженность магнитного поля должна удовлетворять следующим граничным условиям:

1. z=±a   Нх=0 ,

2. z=0     Нх=0 .

Из второго граничного условия следует: С=0. Первое граничное условие ведет к результату:

Скачать файл