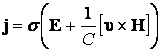 . (13.1.2)
. (13.1.2)
Магнитная гидродинамика как раздел механики
рассматривает лишь такие среды, для которых с большой точностью можно положить:
![]() . Несмотря на это ограничение набор
сред магнитной гидродинамики, имеющих практический интерес достаточно велик.
Это проводящие жидкости, расплавленные металлы, ионизированные газы, плазма.
. Несмотря на это ограничение набор
сред магнитной гидродинамики, имеющих практический интерес достаточно велик.
Это проводящие жидкости, расплавленные металлы, ионизированные газы, плазма.
В магнитной гидродинамике обычно рассматриваются лишь
изотропные среды. Если для ![]() это ограничение
достаточно определенно, то требование изотропности проводимости
это ограничение
достаточно определенно, то требование изотропности проводимости ![]() необходимо рассмотреть более
подробно на микроскопическом уровне. В магнитном поле движущиеся заряды,
обуславливающие ток проводимости, движутся по сложным винтовым траекториям.
Так, частица, имеющая заряд
необходимо рассмотреть более
подробно на микроскопическом уровне. В магнитном поле движущиеся заряды,
обуславливающие ток проводимости, движутся по сложным винтовым траекториям.
Так, частица, имеющая заряд ![]() и массу
и массу ![]() , влетая в однородное магнитное поле
напряженностью
, влетая в однородное магнитное поле
напряженностью ![]() перпендикулярное скорости
частицы, будет вращаться вокруг силовой линии с угловой частотой Лармора
перпендикулярное скорости
частицы, будет вращаться вокруг силовой линии с угловой частотой Лармора ![]() . В то же время заряженная частица,
движущаяся вдоль силовой линии магнитного поля не испытывает со стороны
последнего никакого влияния. Поэтому проводимость среды в магнитном поле может
быть существенно анизотропной. Проводимость вдоль магнитного поля будет
значительно больше чем поперек.
. В то же время заряженная частица,
движущаяся вдоль силовой линии магнитного поля не испытывает со стороны
последнего никакого влияния. Поэтому проводимость среды в магнитном поле может
быть существенно анизотропной. Проводимость вдоль магнитного поля будет
значительно больше чем поперек.
Сравним период Ларморовской прецессии- ![]() и время между двумя
последовательными столкновениями молекул в газе-
и время между двумя
последовательными столкновениями молекул в газе- ![]() .
Очевидно:
.
Очевидно:
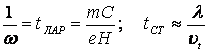 .
.
Здесь
![]() - средняя тепловая скорость частиц.
Не трудно понять, что для того, чтобы проводимость газа была изотропной,
необходимо, чтобы выполнялось следующее условие:
- средняя тепловая скорость частиц.
Не трудно понять, что для того, чтобы проводимость газа была изотропной,
необходимо, чтобы выполнялось следующее условие:
![]() . (13.1.3)
. (13.1.3)
В этом случае частые столкновения частиц не позволят им описывать замкнутые траектории в поперечном магнитном поле. Траектории на малой длине свободного пробега будут почти прямолинейными и определятся столкновением, а не магнитным полем. Следовательно, проводимость будет изотропной, не зависящей от направления магнитного поля.
В магнитогидродинамических задачах обычно пренебрегают токами смещения по сравнению с токами проводимости. Т.е. предполагается что:
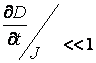 . (13.1.4)
. (13.1.4)
Так, если среда находится в периодическом
электрическом поле ![]() , то отношение амплитуд
равно:
, то отношение амплитуд
равно:
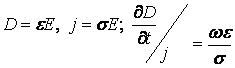 .
.
Поэтому для того чтобы пренебречь токами смещения по
сравнению с токами проводимости необходимо выполнение следующего неравенства: ![]() .
(13.1.5)
.
(13.1.5)
Неравенство (13.1.5) означает, что при заданной проводимости магнитная гидродинамика не рассматривает слишком быстропеременных электромагнитных процессов, при которых ток смещения играл бы существенную или определяющую роль (электромагнитные волны).
Например, проводимость меди равна ![]() , проводимость земной ионосферы
, проводимость земной ионосферы ![]() , проводимость солнечной короны
, проводимость солнечной короны ![]() единиц CGSE. Из формулы
(13.1.5) следует, что ограничение по скорости изменения электродинамических и
механических величин в магнитной гидродинамике не слишком сильное. Поскольку
практически рассматриваются сравнительно медленные движения сплошной среды,
включая и ударные волны, то и вызываемые ими скорости изменения электрических и
магнитных величин практически всегда удовлетворяют неравенству (13.1.5).
единиц CGSE. Из формулы
(13.1.5) следует, что ограничение по скорости изменения электродинамических и
механических величин в магнитной гидродинамике не слишком сильное. Поскольку
практически рассматриваются сравнительно медленные движения сплошной среды,
включая и ударные волны, то и вызываемые ими скорости изменения электрических и
магнитных величин практически всегда удовлетворяют неравенству (13.1.5).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.